TPU에서 폐렴 분류

원본 링크 : https://keras.io/examples/vision/xray_classification_with_tpus/
최종 확인 : 2024-11-20

저자 : Amy MiHyun Jang
생성일 : 2020/07/28
최종 편집일 : 2024/02/12
설명 : TPU에서 의료 이미지 분류.

소개 + 셋업

이 튜토리얼에서는 엑스레이 스캔에서 폐렴(pneumonia)이 있는지 여부를 예측하기 위해, 엑스레이 이미지 분류 모델을 빌드하는 방법을 설명합니다.

import re
import os
import random
import numpy as np
import pandas as pd
import tensorflow as tf
import matplotlib.pyplot as plt

try:
    tpu = tf.distribute.cluster_resolver.TPUClusterResolver.connect()
    print("Device:", tpu.master())
    strategy = tf.distribute.TPUStrategy(tpu)
except:
    strategy = tf.distribute.get_strategy()
print("Number of replicas:", strategy.num_replicas_in_sync)

결과

Device: grpc://10.0.27.122:8470
INFO:tensorflow:Initializing the TPU system: grpc://10.0.27.122:8470

INFO:tensorflow:Initializing the TPU system: grpc://10.0.27.122:8470

INFO:tensorflow:Clearing out eager caches

INFO:tensorflow:Clearing out eager caches

INFO:tensorflow:Finished initializing TPU system.

INFO:tensorflow:Finished initializing TPU system.
WARNING:absl:[`tf.distribute.TPUStrategy`](https://www.tensorflow.org/api_docs/python/tf/distribute/TPUStrategy) is deprecated, please use  the non experimental symbol [`tf.distribute.TPUStrategy`](https://www.tensorflow.org/api_docs/python/tf/distribute/TPUStrategy) instead.

INFO:tensorflow:Found TPU system:

INFO:tensorflow:Found TPU system:

INFO:tensorflow:*** Num TPU Cores: 8

INFO:tensorflow:*** Num TPU Cores: 8

INFO:tensorflow:*** Num TPU Workers: 1

INFO:tensorflow:*** Num TPU Workers: 1

INFO:tensorflow:*** Num TPU Cores Per Worker: 8

INFO:tensorflow:*** Num TPU Cores Per Worker: 8

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:localhost/replica:0/task:0/device:CPU:0, CPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:localhost/replica:0/task:0/device:CPU:0, CPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:localhost/replica:0/task:0/device:XLA_CPU:0, XLA_CPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:localhost/replica:0/task:0/device:XLA_CPU:0, XLA_CPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:CPU:0, CPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:CPU:0, CPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:0, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:0, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:1, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:1, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:2, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:2, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:3, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:3, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:4, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:4, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:5, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:5, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:6, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:6, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:7, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU:7, TPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU_SYSTEM:0, TPU_SYSTEM, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:TPU_SYSTEM:0, TPU_SYSTEM, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:XLA_CPU:0, XLA_CPU, 0, 0)

INFO:tensorflow:*** Available Device: _DeviceAttributes(/job:worker/replica:0/task:0/device:XLA_CPU:0, XLA_CPU, 0, 0)

Number of replicas: 8

TPU를 사용하여 데이터를 로드하려면 데이터에 대한 Google Cloud 링크가 필요합니다. 아래에서는, 이 예제에서 사용할 주요 구성 매개변수를 정의합니다. TPU에서 실행하려면, 이 예제는 TPU 런타임이 선택된 Colab에 있어야 합니다.

AUTOTUNE = tf.data.AUTOTUNE
BATCH_SIZE = 25 * strategy.num_replicas_in_sync
IMAGE_SIZE = [180, 180]
CLASS_NAMES = ["NORMAL", "PNEUMONIA"]

데이터 로드

Cell에서 사용하는 흉부 엑스레이 데이터는 트레이닝 파일과 테스트 파일로 나뉩니다. 먼저 트레이닝용 TFRecords를 로드해 보겠습니다.

train_images = tf.data.TFRecordDataset(
    "gs://download.tensorflow.org/data/ChestXRay2017/train/images.tfrec"
)
train_paths = tf.data.TFRecordDataset(
    "gs://download.tensorflow.org/data/ChestXRay2017/train/paths.tfrec"
)

ds = tf.data.Dataset.zip((train_images, train_paths))

건강한/정상 흉부 엑스레이와 폐렴 흉부 엑스레이의 수를 세어 보겠습니다:

COUNT_NORMAL = len(
    [
        filename
        for filename in train_paths
        if "NORMAL" in filename.numpy().decode("utf-8")
    ]
)
print("Normal images count in training set: " + str(COUNT_NORMAL))

COUNT_PNEUMONIA = len(
    [
        filename
        for filename in train_paths
        if "PNEUMONIA" in filename.numpy().decode("utf-8")
    ]
)
print("Pneumonia images count in training set: " + str(COUNT_PNEUMONIA))

결과

Normal images count in training set: 1349
Pneumonia images count in training set: 3883

폐렴으로 분류된 이미지가 정상보다 훨씬 더 많은 것을 알 수 있습니다. 이는 데이터에 불균형이 있음을 보여줍니다. 이 불균형은 나중에 노트북에서 수정하겠습니다.

각 파일 이름을 해당 (이미지, 레이블) 쌍에 매핑하고 싶습니다. 다음 방법이 도움이 될 것입니다.

레이블이 두 개뿐이므로, 1 또는 True가 폐렴을 나타내고, 0 또는 False가 정상을 나타내도록 레이블을 인코딩합니다.

def get_label(file_path):
    # 경로를 경로 구성 요소 리스트로 변환
    parts = tf.strings.split(file_path, "/")
    # 맨 마지막에서 두 번째는 클래스 디렉터리.
    if parts[-2] == "PNEUMONIA":
        return 1
    else:
        return 0


def decode_img(img):
    # 압축된 문자열을 3D uint8 텐서로 변환.
    img = tf.image.decode_jpeg(img, channels=3)
    # 원하는 크기로 이미지 크기를 조정.
    return tf.image.resize(img, IMAGE_SIZE)


def process_path(image, path):
    label = get_label(path)
    # 파일에서 원시 데이터를 문자열로 로드.
    img = decode_img(image)
    return img, label


ds = ds.map(process_path, num_parallel_calls=AUTOTUNE)

데이터를 트레이닝 데이터 세트와 검증 데이터 세트로 나눠 보겠습니다.

ds = ds.shuffle(10000)
train_ds = ds.take(4200)
val_ds = ds.skip(4200)

(이미지, 레이블) 쌍의 모양을 시각화해 보겠습니다.

for image, label in train_ds.take(1):
    print("Image shape: ", image.numpy().shape)
    print("Label: ", label.numpy())

결과

Image shape:  (180, 180, 3)
Label:  False

테스트 데이터도 로드하고 서식을 지정합니다.

test_images = tf.data.TFRecordDataset(
    "gs://download.tensorflow.org/data/ChestXRay2017/test/images.tfrec"
)
test_paths = tf.data.TFRecordDataset(
    "gs://download.tensorflow.org/data/ChestXRay2017/test/paths.tfrec"
)
test_ds = tf.data.Dataset.zip((test_images, test_paths))

test_ds = test_ds.map(process_path, num_parallel_calls=AUTOTUNE)
test_ds = test_ds.batch(BATCH_SIZE)

데이터세트 시각화

먼저, 버퍼링된 프리페칭을 사용하여 I/O가 차단되지 않고 디스크에서 데이터를 가져올 수 있도록 하겠습니다.

대용량 이미지 데이터세트는 메모리에 캐시해서는 안 된다는 점에 유의하세요. 여기서는 데이터 세트가 그다지 크지 않고, TPU에서 트레이닝을 하고자 하기 때문에 이렇게 합니다.

def prepare_for_training(ds, cache=True):
    # 작은 데이터 집합이므로, 한 번만 로드하고, 메모리에 보관합니다.
    # 메모리에 맞지 않는 데이터 집합의 전처리 작업을 캐시하려면 `.cache(filename)`를 사용합니다.
    if cache:
        if isinstance(cache, str):
            ds = ds.cache(cache)
        else:
            ds = ds.cache()

    ds = ds.batch(BATCH_SIZE)

    # `prefetch`는 모델이 트레이닝하는 동안 데이터세트가 백그라운드에서 배치를 가져올 수 있도록 합니다.
    ds = ds.prefetch(buffer_size=AUTOTUNE)

    return ds

트레이닝 데이터의 다음 배치 반복을 호출합니다.

train_ds = prepare_for_training(train_ds)
val_ds = prepare_for_training(val_ds)

image_batch, label_batch = next(iter(train_ds))

배치에 이미지를 표시하는 방법을 정의합니다.

def show_batch(image_batch, label_batch):
    plt.figure(figsize=(10, 10))
    for n in range(25):
        ax = plt.subplot(5, 5, n + 1)
        plt.imshow(image_batch[n] / 255)
        if label_batch[n]:
            plt.title("PNEUMONIA")
        else:
            plt.title("NORMAL")
        plt.axis("off")

이 메서드는 매개변수로 NumPy 배열을 받으므로, 배치에서 numpy 함수를 호출하여 텐서를 NumPy 배열 형식으로 반환합니다.

show_batch(image_batch.numpy(), label_batch.numpy())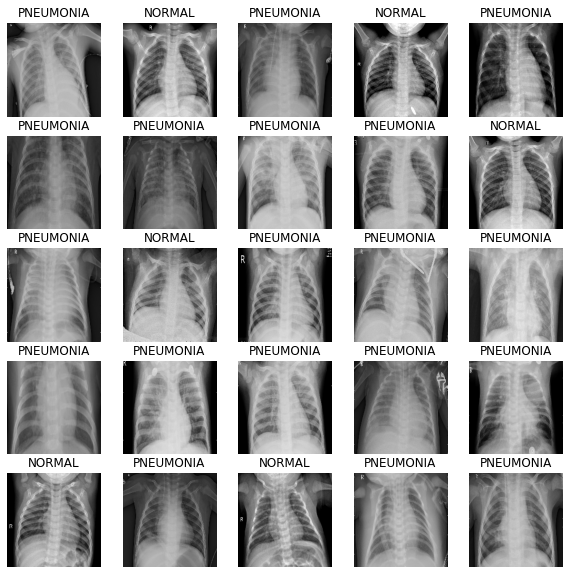

png

CNN 빌드

모델을 보다 모듈화하고 이해하기 쉽게 만들기 위해, 몇 가지 블록을 정의해 보겠습니다. 컨볼루션 신경망을 빌드할 때, 컨볼루션 블록과 Dense 레이어 블록을 만들겠습니다.

이 CNN의 아키텍처는 이 글에서 영감을 얻었습니다.

import os
os.environ['KERAS_BACKEND'] = 'tensorflow'

import keras
from keras import layers

def conv_block(filters, inputs):
    x = layers.SeparableConv2D(filters, 3, activation="relu", padding="same")(inputs)
    x = layers.SeparableConv2D(filters, 3, activation="relu", padding="same")(x)
    x = layers.BatchNormalization()(x)
    outputs = layers.MaxPool2D()(x)

    return outputs


def dense_block(units, dropout_rate, inputs):
    x = layers.Dense(units, activation="relu")(inputs)
    x = layers.BatchNormalization()(x)
    outputs = layers.Dropout(dropout_rate)(x)

    return outputs

다음 메서드는 모델을 빌드하는 함수를 정의합니다.

이미지의 원래 값은 [0, 255] 범위입니다. CNN은 숫자가 작을수록 더 잘 작동하므로, 입력에 맞게 이 값을 축소하겠습니다.

드롭아웃 레이어는 모델이 과적합할 가능성을 줄여주기 때문에 중요합니다. 노드가 하나 있는 Dense 레이어로 모델을 끝내고자 하는데, 이는 엑스레이에서 폐렴의 존재 여부를 판단하는 이진 출력이 될 것이기 때문입니다.

def build_model():
    inputs = keras.Input(shape=(IMAGE_SIZE[0], IMAGE_SIZE[1], 3))
    x = layers.Rescaling(1.0 / 255)(inputs)
    x = layers.Conv2D(16, 3, activation="relu", padding="same")(x)
    x = layers.Conv2D(16, 3, activation="relu", padding="same")(x)
    x = layers.MaxPool2D()(x)

    x = conv_block(32, x)
    x = conv_block(64, x)

    x = conv_block(128, x)
    x = layers.Dropout(0.2)(x)

    x = conv_block(256, x)
    x = layers.Dropout(0.2)(x)

    x = layers.Flatten()(x)
    x = dense_block(512, 0.7, x)
    x = dense_block(128, 0.5, x)
    x = dense_block(64, 0.3, x)

    outputs = layers.Dense(1, activation="sigmoid")(x)

    model = keras.Model(inputs=inputs, outputs=outputs)
    return model

데이터 불균형 수정

이 예제 앞부분에서, 폐렴으로 분류된 이미지가 정상보다 많아 데이터의 불균형을 확인했습니다. 클래스 가중치를 사용하여 이를 보정하겠습니다:

initial_bias = np.log([COUNT_PNEUMONIA / COUNT_NORMAL])
print("Initial bias: {:.5f}".format(initial_bias[0]))

TRAIN_IMG_COUNT = COUNT_NORMAL + COUNT_PNEUMONIA
weight_for_0 = (1 / COUNT_NORMAL) * (TRAIN_IMG_COUNT) / 2.0
weight_for_1 = (1 / COUNT_PNEUMONIA) * (TRAIN_IMG_COUNT) / 2.0

class_weight = {0: weight_for_0, 1: weight_for_1}

print("Weight for class 0: {:.2f}".format(weight_for_0))
print("Weight for class 1: {:.2f}".format(weight_for_1))

결과

Initial bias: 1.05724
Weight for class 0: 1.94
Weight for class 1: 0.67

클래스 0(정상)의 가중치가 클래스 1(폐렴)의 가중치보다 훨씬 높습니다. 트레이닝 데이터가 균형을 이룰 때 CNN이 가장 잘 작동하므로, 정상 이미지가 적기 때문에 각 정상 이미지에 더 많은 가중치를 부여하여 데이터의 균형을 맞춥니다.

모델 트레이닝

콜백 정의하기

체크포인트 콜백은 모델의 가장 좋은 가중치를 저장하므로, 다음에 모델을 사용하고자 할 때, 트레이닝에 시간을 들일 필요가 없습니다. 조기 중지 콜백은 모델이 정체되기 시작하거나, 모델이 과적합하기 시작하면 트레이닝 프로세스를 중지합니다.

checkpoint_cb = keras.callbacks.ModelCheckpoint("xray_model.keras", save_best_only=True)

early_stopping_cb = keras.callbacks.EarlyStopping(
    patience=10, restore_best_weights=True
)

학습률도 조정하고 싶습니다. 학습률이 너무 높으면 모델이 발산(diverge)될 수 있습니다. 학습률이 너무 작으면, 모델이 너무 느려집니다. 아래에서 지수 학습률 스케줄링 방법을 구현합니다.

initial_learning_rate = 0.015
lr_schedule = keras.optimizers.schedules.ExponentialDecay(
    initial_learning_rate, decay_steps=100000, decay_rate=0.96, staircase=True
)

모델 Fit

메트릭에는, 정확도(precision)와 재응답률(recall)이 포함되어야 모델이 얼마나 좋은지 더 많은 정보를 얻을 수 있습니다. 정확도는 레이블 중 몇 퍼센트의 레이블이 정확한지를 알려줍니다. 데이터의 균형이 맞지 않기 때문에, 정확도는 좋은 모델에 대한 왜곡된 느낌을 줄 수 있습니다. (즉, PNEUMONIA를 항상 74% 정확도로 예측하는 모델은 좋은 모델이 아닙니다)

정확도(Precision)는 TP(true positives)와 FP(false negatves)의 합에 대한 TP의 수입니다. 이는 라벨이 지정된 양성 중 실제로 정확한 비율을 보여줍니다.

리콜(Recall)은 TP와 FN의 합에 대한 TP의 수입니다. 실제 양성 중 몇 퍼센트가 정확한지를 보여줍니다.

이미지에 가능한 레이블이 두 개뿐이므로, 이진 교차 엔트로피 손실을 사용하겠습니다. 모델을 fit 할 때, 앞서 정의한 클래스 가중치를 지정하는 것을 잊지 마세요. TPU를 사용하기 때문에, 트레이닝은 2분 이내에 빠르게 완료됩니다.

with strategy.scope():
    model = build_model()

    METRICS = [
        keras.metrics.BinaryAccuracy(),
        keras.metrics.Precision(name="precision"),
        keras.metrics.Recall(name="recall"),
    ]
    model.compile(
        optimizer=keras.optimizers.Adam(learning_rate=lr_schedule),
        loss="binary_crossentropy",
        metrics=METRICS,
    )

history = model.fit(
    train_ds,
    epochs=100,
    validation_data=val_ds,
    class_weight=class_weight,
    callbacks=[checkpoint_cb, early_stopping_cb],
)

결과

Epoch 1/100
WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/data/ops/multi_device_iterator_ops.py:601: get_next_as_optional (from tensorflow.python.data.ops.iterator_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use `tf.data.Iterator.get_next_as_optional()` instead.

WARNING:tensorflow:From /usr/local/lib/python3.6/dist-packages/tensorflow/python/data/ops/multi_device_iterator_ops.py:601: get_next_as_optional (from tensorflow.python.data.ops.iterator_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use `tf.data.Iterator.get_next_as_optional()` instead.

21/21 [==============================] - 12s 568ms/step - loss: 0.5857 - binary_accuracy: 0.6960 - precision: 0.8887 - recall: 0.6733 - val_loss: 34.0149 - val_binary_accuracy: 0.7180 - val_precision: 0.7180 - val_recall: 1.0000
Epoch 2/100
21/21 [==============================] - 3s 128ms/step - loss: 0.2916 - binary_accuracy: 0.8755 - precision: 0.9540 - recall: 0.8738 - val_loss: 97.5194 - val_binary_accuracy: 0.7180 - val_precision: 0.7180 - val_recall: 1.0000
Epoch 3/100
21/21 [==============================] - 4s 167ms/step - loss: 0.2384 - binary_accuracy: 0.9002 - precision: 0.9663 - recall: 0.8964 - val_loss: 27.7902 - val_binary_accuracy: 0.7180 - val_precision: 0.7180 - val_recall: 1.0000
Epoch 4/100
21/21 [==============================] - 4s 173ms/step - loss: 0.2046 - binary_accuracy: 0.9145 - precision: 0.9725 - recall: 0.9102 - val_loss: 10.8302 - val_binary_accuracy: 0.7180 - val_precision: 0.7180 - val_recall: 1.0000
Epoch 5/100
21/21 [==============================] - 4s 174ms/step - loss: 0.1841 - binary_accuracy: 0.9279 - precision: 0.9733 - recall: 0.9279 - val_loss: 3.5860 - val_binary_accuracy: 0.7103 - val_precision: 0.7162 - val_recall: 0.9879
Epoch 6/100
21/21 [==============================] - 4s 185ms/step - loss: 0.1600 - binary_accuracy: 0.9362 - precision: 0.9791 - recall: 0.9337 - val_loss: 0.3014 - val_binary_accuracy: 0.8895 - val_precision: 0.8973 - val_recall: 0.9555
Epoch 7/100
21/21 [==============================] - 3s 130ms/step - loss: 0.1567 - binary_accuracy: 0.9393 - precision: 0.9798 - recall: 0.9372 - val_loss: 0.6763 - val_binary_accuracy: 0.7810 - val_precision: 0.7760 - val_recall: 0.9771
Epoch 8/100
21/21 [==============================] - 3s 131ms/step - loss: 0.1532 - binary_accuracy: 0.9421 - precision: 0.9825 - recall: 0.9385 - val_loss: 0.3169 - val_binary_accuracy: 0.8895 - val_precision: 0.8684 - val_recall: 0.9973
Epoch 9/100
21/21 [==============================] - 4s 184ms/step - loss: 0.1457 - binary_accuracy: 0.9431 - precision: 0.9822 - recall: 0.9401 - val_loss: 0.2064 - val_binary_accuracy: 0.9273 - val_precision: 0.9840 - val_recall: 0.9136
Epoch 10/100
21/21 [==============================] - 3s 132ms/step - loss: 0.1201 - binary_accuracy: 0.9521 - precision: 0.9869 - recall: 0.9479 - val_loss: 0.4364 - val_binary_accuracy: 0.8605 - val_precision: 0.8443 - val_recall: 0.9879
Epoch 11/100
21/21 [==============================] - 3s 127ms/step - loss: 0.1200 - binary_accuracy: 0.9510 - precision: 0.9863 - recall: 0.9469 - val_loss: 0.5197 - val_binary_accuracy: 0.8508 - val_precision: 1.0000 - val_recall: 0.7922
Epoch 12/100
21/21 [==============================] - 4s 186ms/step - loss: 0.1077 - binary_accuracy: 0.9581 - precision: 0.9870 - recall: 0.9559 - val_loss: 0.1349 - val_binary_accuracy: 0.9486 - val_precision: 0.9587 - val_recall: 0.9703
Epoch 13/100
21/21 [==============================] - 4s 173ms/step - loss: 0.0918 - binary_accuracy: 0.9650 - precision: 0.9914 - recall: 0.9611 - val_loss: 0.0926 - val_binary_accuracy: 0.9700 - val_precision: 0.9837 - val_recall: 0.9744
Epoch 14/100
21/21 [==============================] - 3s 130ms/step - loss: 0.0996 - binary_accuracy: 0.9612 - precision: 0.9913 - recall: 0.9559 - val_loss: 0.1811 - val_binary_accuracy: 0.9419 - val_precision: 0.9956 - val_recall: 0.9231
Epoch 15/100
21/21 [==============================] - 3s 129ms/step - loss: 0.0898 - binary_accuracy: 0.9643 - precision: 0.9901 - recall: 0.9614 - val_loss: 0.1525 - val_binary_accuracy: 0.9486 - val_precision: 0.9986 - val_recall: 0.9298
Epoch 16/100
21/21 [==============================] - 3s 128ms/step - loss: 0.0941 - binary_accuracy: 0.9621 - precision: 0.9904 - recall: 0.9582 - val_loss: 0.5101 - val_binary_accuracy: 0.8527 - val_precision: 1.0000 - val_recall: 0.7949
Epoch 17/100
21/21 [==============================] - 3s 125ms/step - loss: 0.0798 - binary_accuracy: 0.9636 - precision: 0.9897 - recall: 0.9607 - val_loss: 0.1239 - val_binary_accuracy: 0.9622 - val_precision: 0.9875 - val_recall: 0.9595
Epoch 18/100
21/21 [==============================] - 3s 126ms/step - loss: 0.0821 - binary_accuracy: 0.9657 - precision: 0.9911 - recall: 0.9623 - val_loss: 0.1597 - val_binary_accuracy: 0.9322 - val_precision: 0.9956 - val_recall: 0.9096
Epoch 19/100
21/21 [==============================] - 3s 143ms/step - loss: 0.0800 - binary_accuracy: 0.9657 - precision: 0.9917 - recall: 0.9617 - val_loss: 0.2538 - val_binary_accuracy: 0.9109 - val_precision: 1.0000 - val_recall: 0.8758
Epoch 20/100
21/21 [==============================] - 3s 127ms/step - loss: 0.0605 - binary_accuracy: 0.9738 - precision: 0.9950 - recall: 0.9694 - val_loss: 0.6594 - val_binary_accuracy: 0.8566 - val_precision: 1.0000 - val_recall: 0.8003
Epoch 21/100
21/21 [==============================] - 4s 167ms/step - loss: 0.0726 - binary_accuracy: 0.9733 - precision: 0.9937 - recall: 0.9701 - val_loss: 0.0593 - val_binary_accuracy: 0.9816 - val_precision: 0.9945 - val_recall: 0.9798
Epoch 22/100
21/21 [==============================] - 3s 126ms/step - loss: 0.0577 - binary_accuracy: 0.9783 - precision: 0.9951 - recall: 0.9755 - val_loss: 0.1087 - val_binary_accuracy: 0.9729 - val_precision: 0.9931 - val_recall: 0.9690
Epoch 23/100
21/21 [==============================] - 3s 125ms/step - loss: 0.0652 - binary_accuracy: 0.9729 - precision: 0.9924 - recall: 0.9707 - val_loss: 1.8465 - val_binary_accuracy: 0.7180 - val_precision: 0.7180 - val_recall: 1.0000
Epoch 24/100
21/21 [==============================] - 3s 124ms/step - loss: 0.0538 - binary_accuracy: 0.9783 - precision: 0.9951 - recall: 0.9755 - val_loss: 1.5769 - val_binary_accuracy: 0.7180 - val_precision: 0.7180 - val_recall: 1.0000
Epoch 25/100
21/21 [==============================] - 4s 167ms/step - loss: 0.0549 - binary_accuracy: 0.9776 - precision: 0.9954 - recall: 0.9743 - val_loss: 0.0590 - val_binary_accuracy: 0.9777 - val_precision: 0.9904 - val_recall: 0.9784
Epoch 26/100
21/21 [==============================] - 3s 131ms/step - loss: 0.0677 - binary_accuracy: 0.9719 - precision: 0.9924 - recall: 0.9694 - val_loss: 2.6008 - val_binary_accuracy: 0.6928 - val_precision: 0.9977 - val_recall: 0.5735
Epoch 27/100
21/21 [==============================] - 3s 127ms/step - loss: 0.0469 - binary_accuracy: 0.9833 - precision: 0.9971 - recall: 0.9804 - val_loss: 1.0184 - val_binary_accuracy: 0.8605 - val_precision: 0.9983 - val_recall: 0.8070
Epoch 28/100
21/21 [==============================] - 3s 126ms/step - loss: 0.0501 - binary_accuracy: 0.9790 - precision: 0.9961 - recall: 0.9755 - val_loss: 0.3737 - val_binary_accuracy: 0.9089 - val_precision: 0.9954 - val_recall: 0.8772
Epoch 29/100
21/21 [==============================] - 3s 128ms/step - loss: 0.0548 - binary_accuracy: 0.9798 - precision: 0.9941 - recall: 0.9784 - val_loss: 1.2928 - val_binary_accuracy: 0.7907 - val_precision: 1.0000 - val_recall: 0.7085
Epoch 30/100
21/21 [==============================] - 3s 129ms/step - loss: 0.0370 - binary_accuracy: 0.9860 - precision: 0.9980 - recall: 0.9829 - val_loss: 0.1370 - val_binary_accuracy: 0.9612 - val_precision: 0.9972 - val_recall: 0.9487
Epoch 31/100
21/21 [==============================] - 3s 125ms/step - loss: 0.0585 - binary_accuracy: 0.9819 - precision: 0.9951 - recall: 0.9804 - val_loss: 1.1955 - val_binary_accuracy: 0.6870 - val_precision: 0.9976 - val_recall: 0.5655
Epoch 32/100
21/21 [==============================] - 3s 140ms/step - loss: 0.0813 - binary_accuracy: 0.9695 - precision: 0.9934 - recall: 0.9652 - val_loss: 1.0394 - val_binary_accuracy: 0.8576 - val_precision: 0.9853 - val_recall: 0.8138
Epoch 33/100
21/21 [==============================] - 3s 128ms/step - loss: 0.1111 - binary_accuracy: 0.9555 - precision: 0.9870 - recall: 0.9524 - val_loss: 4.9438 - val_binary_accuracy: 0.5911 - val_precision: 1.0000 - val_recall: 0.4305
Epoch 34/100
21/21 [==============================] - 3s 130ms/step - loss: 0.0680 - binary_accuracy: 0.9726 - precision: 0.9921 - recall: 0.9707 - val_loss: 2.8822 - val_binary_accuracy: 0.7267 - val_precision: 0.9978 - val_recall: 0.6208
Epoch 35/100
21/21 [==============================] - 4s 187ms/step - loss: 0.0784 - binary_accuracy: 0.9712 - precision: 0.9892 - recall: 0.9717 - val_loss: 0.3940 - val_binary_accuracy: 0.9390 - val_precision: 0.9942 - val_recall: 0.9204

모델 성능 시각화

트레이닝 및 검증 세트에 대한 모델 정확도와 손실을 플로팅해 보겠습니다. 이 노트북에는 랜덤 시드가 지정되어 있지 않습니다. 노트북의 경우, 약간의 편차가 있을 수 있습니다.

fig, ax = plt.subplots(1, 4, figsize=(20, 3))
ax = ax.ravel()

for i, met in enumerate(["precision", "recall", "binary_accuracy", "loss"]):
    ax[i].plot(history.history[met])
    ax[i].plot(history.history["val_" + met])
    ax[i].set_title("Model {}".format(met))
    ax[i].set_xlabel("epochs")
    ax[i].set_ylabel(met)
    ax[i].legend(["train", "val"])

png

저희 모델의 정확도는 약 95%입니다.

결과 예측 및 평가

테스트 데이터로 모델을 평가해 봅시다!

model.evaluate(test_ds, return_dict=True)

결과

4/4 [==============================] - 3s 708ms/step - loss: 0.9718 - binary_accuracy: 0.7901 - precision: 0.7524 - recall: 0.9897

{'binary_accuracy': 0.7900640964508057,
 'loss': 0.9717951416969299,
 'precision': 0.752436637878418,
 'recall': 0.9897436499595642}

테스트 데이터의 정확도가 검증 집합의 정확도보다 낮다는 것을 알 수 있습니다. 이는 과적합을 나타낼 수 있습니다.

정확도(precision)보다 리콜(recall)이 더 높다는 것은, 거의 모든 폐렴 이미지를 정확하게 식별했지만, 일부 정상 이미지를 잘못 식별했음을 나타냅니다. 정확도(precision)를 높이는 것을 목표로 해야 합니다.

for image, label in test_ds.take(1):
    plt.imshow(image[0] / 255.0)
    plt.title(CLASS_NAMES[label[0].numpy()])

prediction = model.predict(test_ds.take(1))[0]
scores = [1 - prediction, prediction]

for score, name in zip(scores, CLASS_NAMES):
    print("This image is %.2f percent %s" % ((100 * score), name))

결과

/usr/local/lib/python3.6/dist-packages/ipykernel_launcher.py:3: DeprecationWarning: In future, it will be an error for 'np.bool_' scalars to be interpreted as an index
  This is separate from the ipykernel package so we can avoid doing imports until

This image is 47.19 percent NORMAL
This image is 52.81 percent PNEUMONIA

png