Swin 트랜스포머를 사용한 이미지 분류
- 원본 링크 : https://keras.io/examples/vision/swin_transformers/
- 최종 확인 : 2024-11-20
저자 : Rishit Dagli
생성일 : 2021/09/08
최종 편집일 : 2021/09/08
설명 : 컴퓨터 비전용 범용 백본인 Swin Transformers를 사용한 이미지 분류.
이 예제는 Liu 등의 Swin Transformer: Shifted 윈도우를 사용한 계층적 비전 트랜스포머(Swin Transformer: Hierarchical Vision Transformer using Shifted Windows)를 이미지 분류를 위해 구현하고, CIFAR-100 데이터셋에 대해 시연합니다.
Swin Transformer (Shifted Window Transformer)는 컴퓨터 비전을 위한 범용 백본으로 사용될 수 있습니다. Swin Transformer는 이동된 윈도우(shifted windows) 로 표현을 계산하는 계층적 트랜스포머입니다. Shifted Windows 방식은 셀프 어텐션 계산을 겹치지 않는 지역 윈도우로 제한하면서도, 윈도우 간 연결을 허용함으로써 더 큰 효율성을 가져옵니다. 이 아키텍처는 다양한 스케일의 정보를 모델링할 수 있는 유연성을 가지며, 이미지 크기에 대해 선형적인 계산 복잡도를 가집니다.
이 예제는 TensorFlow 2.5 이상이 필요합니다.
셋업
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf # tf.data 및 전처리에만 해당됩니다.
import keras
from keras import layers
from keras import ops하이퍼파라미터 구성
A key parameter to pick is the patch_size, the size of the input patches. In order to use each pixel as an individual input, you can set patch_size to (1, 1). Below, we take inspiration from the original paper settings for training on ImageNet-1K, keeping most of the original settings for this example.
선택할 주요 매개변수는 입력 패치의 크기인 patch_size입니다.
각 픽셀을 개별 입력으로 사용하려면, patch_size를 (1, 1)로 설정하면 됩니다.
아래에서는, ImageNet-1K 트레이닝을 위한 원본 논문 설정에서 영감을 얻어,
이 예제에서는 원본 설정을 대부분 유지합니다.
num_classes = 100
input_shape = (32, 32, 3)
patch_size = (2, 2) # 2x2 크기의 패치
dropout_rate = 0.03 # Dropout 비율
num_heads = 8 # 어텐션 헤드
embed_dim = 64 # 임베딩 차원
num_mlp = 256 # MLP 레이어 크기
# 학습 가능한 추가적인 값을 사용하여 임베디드 패치를 쿼리, 키 및 값으로 변환
qkv_bias = True
window_size = 2 # 어텐션 윈도우의 크기
shift_size = 1 # 이동 윈도우의 크기
image_dimension = 32 # 초기 이미지 크기
num_patch_x = input_shape[0] // patch_size[0]
num_patch_y = input_shape[1] // patch_size[1]
learning_rate = 1e-3
batch_size = 128
num_epochs = 40
validation_split = 0.1
weight_decay = 0.0001
label_smoothing = 0.1데이터 준비
CIFAR-100 데이터셋을 keras.datasets를 통해 로드하고,
이미지를 정규화하고, 정수 레이블을 원-핫 인코딩된 벡터로 변환합니다.
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar100.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
num_train_samples = int(len(x_train) * (1 - validation_split))
num_val_samples = len(x_train) - num_train_samples
x_train, x_val = np.split(x_train, [num_train_samples])
y_train, y_val = np.split(y_train, [num_train_samples])
print(f"x_train shape: {x_train.shape} - y_train shape: {y_train.shape}")
print(f"x_test shape: {x_test.shape} - y_test shape: {y_test.shape}")
plt.figure(figsize=(10, 10))
for i in range(25):
plt.subplot(5, 5, i + 1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(x_train[i])
plt.show()결과
x_train shape: (45000, 32, 32, 3) - y_train shape: (45000, 100)
x_test shape: (10000, 32, 32, 3) - y_test shape: (10000, 100)
헬퍼 함수
이미지에서 패치 시퀀스를 얻고, 패치를 병합하고, 드롭아웃을 적용하는 두 개의 헬퍼 함수를 만듭니다.
def window_partition(x, window_size):
_, height, width, channels = x.shape
patch_num_y = height // window_size
patch_num_x = width // window_size
x = ops.reshape(
x,
(
-1,
patch_num_y,
window_size,
patch_num_x,
window_size,
channels,
),
)
x = ops.transpose(x, (0, 1, 3, 2, 4, 5))
windows = ops.reshape(x, (-1, window_size, window_size, channels))
return windows
def window_reverse(windows, window_size, height, width, channels):
patch_num_y = height // window_size
patch_num_x = width // window_size
x = ops.reshape(
windows,
(
-1,
patch_num_y,
patch_num_x,
window_size,
window_size,
channels,
),
)
x = ops.transpose(x, (0, 1, 3, 2, 4, 5))
x = ops.reshape(x, (-1, height, width, channels))
return x윈도우 기반 멀티 헤드 셀프 어텐션
일반적으로 트랜스포머는 글로벌 셀프 어텐션을 수행하여, 토큰과 다른 모든 토큰 간의 관계를 계산합니다. 글로벌 계산은 토큰 수에 대해 이차적인 복잡도로 이어집니다. 여기서는, 원본 논문이 제안하는대로, 겹치지 않는 방식으로, 로컬 윈도우 내에서 셀프 어텐션을 계산합니다. 글로벌 셀프 어텐션은 패치 수에 대해 이차적인 계산 복잡도를 가지지만, 윈도우 기반 셀프 어텐션은 선형적인 복잡도를 가지며 쉽게 확장 가능합니다.
class WindowAttention(layers.Layer):
def __init__(
self,
dim,
window_size,
num_heads,
qkv_bias=True,
dropout_rate=0.0,
**kwargs,
):
super().__init__(**kwargs)
self.dim = dim
self.window_size = window_size
self.num_heads = num_heads
self.scale = (dim // num_heads) ** -0.5
self.qkv = layers.Dense(dim * 3, use_bias=qkv_bias)
self.dropout = layers.Dropout(dropout_rate)
self.proj = layers.Dense(dim)
num_window_elements = (2 * self.window_size[0] - 1) * (
2 * self.window_size[1] - 1
)
self.relative_position_bias_table = self.add_weight(
shape=(num_window_elements, self.num_heads),
initializer=keras.initializers.Zeros(),
trainable=True,
)
coords_h = np.arange(self.window_size[0])
coords_w = np.arange(self.window_size[1])
coords_matrix = np.meshgrid(coords_h, coords_w, indexing="ij")
coords = np.stack(coords_matrix)
coords_flatten = coords.reshape(2, -1)
relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]
relative_coords = relative_coords.transpose([1, 2, 0])
relative_coords[:, :, 0] += self.window_size[0] - 1
relative_coords[:, :, 1] += self.window_size[1] - 1
relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
relative_position_index = relative_coords.sum(-1)
self.relative_position_index = keras.Variable(
initializer=relative_position_index,
shape=relative_position_index.shape,
dtype="int",
trainable=False,
)
def call(self, x, mask=None):
_, size, channels = x.shape
head_dim = channels // self.num_heads
x_qkv = self.qkv(x)
x_qkv = ops.reshape(x_qkv, (-1, size, 3, self.num_heads, head_dim))
x_qkv = ops.transpose(x_qkv, (2, 0, 3, 1, 4))
q, k, v = x_qkv[0], x_qkv[1], x_qkv[2]
q = q * self.scale
k = ops.transpose(k, (0, 1, 3, 2))
attn = q @ k
num_window_elements = self.window_size[0] * self.window_size[1]
relative_position_index_flat = ops.reshape(self.relative_position_index, (-1,))
relative_position_bias = ops.take(
self.relative_position_bias_table,
relative_position_index_flat,
axis=0,
)
relative_position_bias = ops.reshape(
relative_position_bias,
(num_window_elements, num_window_elements, -1),
)
relative_position_bias = ops.transpose(relative_position_bias, (2, 0, 1))
attn = attn + ops.expand_dims(relative_position_bias, axis=0)
if mask is not None:
nW = mask.shape[0]
mask_float = ops.cast(
ops.expand_dims(ops.expand_dims(mask, axis=1), axis=0),
"float32",
)
attn = ops.reshape(attn, (-1, nW, self.num_heads, size, size)) + mask_float
attn = ops.reshape(attn, (-1, self.num_heads, size, size))
attn = keras.activations.softmax(attn, axis=-1)
else:
attn = keras.activations.softmax(attn, axis=-1)
attn = self.dropout(attn)
x_qkv = attn @ v
x_qkv = ops.transpose(x_qkv, (0, 2, 1, 3))
x_qkv = ops.reshape(x_qkv, (-1, size, channels))
x_qkv = self.proj(x_qkv)
x_qkv = self.dropout(x_qkv)
return x_qkv완전한 Swin Transformer 모델
마지막으로, 표준 멀티 헤드 어텐션(MHA, multi-head attention)를
이동된 윈도우 어텐션으로 대체하여 완전한 Swin Transformer를 구성합니다.
원본 논문에서 제안한 대로, 이동된 윈도우 기반 MHA 레이어 다음에,
GELU 비선형성을 가진 2-레이어 MLP를 사용하고,
각 MSA 레이어와 각 MLP 전에 LayerNormalization을 적용하며,
이 레이어들 각각 후에 residual 연결을 적용하는 모델을 만듭니다.
단순히 2개의 Dense 레이어와 2개의 Dropout 레이어로 구성된 간단한 MLP만 만든다는 점에 주목하세요. 종종 문헌에서 매우 표준적인 ResNet-50을 MLP로 사용하는 모델을 볼 수 있습니다. 그러나 이 논문에서 저자들은 중간에 GELU 비선형성을 가진 2-레이어 MLP를 사용합니다.
class SwinTransformer(layers.Layer):
def __init__(
self,
dim,
num_patch,
num_heads,
window_size=7,
shift_size=0,
num_mlp=1024,
qkv_bias=True,
dropout_rate=0.0,
**kwargs,
):
super().__init__(**kwargs)
self.dim = dim # 입력 차원 수
self.num_patch = num_patch # 임베드 패치 수
self.num_heads = num_heads # 어텐션 헤드 수
self.window_size = window_size # 윈도우 크기
self.shift_size = shift_size # 윈도우 shift 크기
self.num_mlp = num_mlp # MLP 노드 수
self.norm1 = layers.LayerNormalization(epsilon=1e-5)
self.attn = WindowAttention(
dim,
window_size=(self.window_size, self.window_size),
num_heads=num_heads,
qkv_bias=qkv_bias,
dropout_rate=dropout_rate,
)
self.drop_path = layers.Dropout(dropout_rate)
self.norm2 = layers.LayerNormalization(epsilon=1e-5)
self.mlp = keras.Sequential(
[
layers.Dense(num_mlp),
layers.Activation(keras.activations.gelu),
layers.Dropout(dropout_rate),
layers.Dense(dim),
layers.Dropout(dropout_rate),
]
)
if min(self.num_patch) < self.window_size:
self.shift_size = 0
self.window_size = min(self.num_patch)
def build(self, input_shape):
if self.shift_size == 0:
self.attn_mask = None
else:
height, width = self.num_patch
h_slices = (
slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None),
)
w_slices = (
slice(0, -self.window_size),
slice(-self.window_size, -self.shift_size),
slice(-self.shift_size, None),
)
mask_array = np.zeros((1, height, width, 1))
count = 0
for h in h_slices:
for w in w_slices:
mask_array[:, h, w, :] = count
count += 1
mask_array = ops.convert_to_tensor(mask_array)
# 배열을 윈도우에 마스크
mask_windows = window_partition(mask_array, self.window_size)
mask_windows = ops.reshape(
mask_windows, [-1, self.window_size * self.window_size]
)
attn_mask = ops.expand_dims(mask_windows, axis=1) - ops.expand_dims(
mask_windows, axis=2
)
attn_mask = ops.where(attn_mask != 0, -100.0, attn_mask)
attn_mask = ops.where(attn_mask == 0, 0.0, attn_mask)
self.attn_mask = keras.Variable(
initializer=attn_mask,
shape=attn_mask.shape,
dtype=attn_mask.dtype,
trainable=False,
)
def call(self, x, training=False):
height, width = self.num_patch
_, num_patches_before, channels = x.shape
x_skip = x
x = self.norm1(x)
x = ops.reshape(x, (-1, height, width, channels))
if self.shift_size > 0:
shifted_x = ops.roll(
x, shift=[-self.shift_size, -self.shift_size], axis=[1, 2]
)
else:
shifted_x = x
x_windows = window_partition(shifted_x, self.window_size)
x_windows = ops.reshape(
x_windows, (-1, self.window_size * self.window_size, channels)
)
attn_windows = self.attn(x_windows, mask=self.attn_mask)
attn_windows = ops.reshape(
attn_windows,
(-1, self.window_size, self.window_size, channels),
)
shifted_x = window_reverse(
attn_windows, self.window_size, height, width, channels
)
if self.shift_size > 0:
x = ops.roll(
shifted_x, shift=[self.shift_size, self.shift_size], axis=[1, 2]
)
else:
x = shifted_x
x = ops.reshape(x, (-1, height * width, channels))
x = self.drop_path(x, training=training)
x = x_skip + x
x_skip = x
x = self.norm2(x)
x = self.mlp(x)
x = self.drop_path(x)
x = x_skip + x
return x모델 트레이닝 및 평가
추출 및 패치 임베딩
우선, 이미지에서 패치를 추출하고, 임베딩하며 병합하는 데 도움이 되는 3개의 레이어를 만듭니다. 이후에 우리가 구축한 Swin Transformer 클래스를 사용할 것입니다.
# tf.data에서만 사용되므로 tf ops를 사용합니다.
def patch_extract(images):
batch_size = tf.shape(images)[0]
patches = tf.image.extract_patches(
images=images,
sizes=(1, patch_size[0], patch_size[1], 1),
strides=(1, patch_size[0], patch_size[1], 1),
rates=(1, 1, 1, 1),
padding="VALID",
)
patch_dim = patches.shape[-1]
patch_num = patches.shape[1]
return tf.reshape(patches, (batch_size, patch_num * patch_num, patch_dim))
class PatchEmbedding(layers.Layer):
def __init__(self, num_patch, embed_dim, **kwargs):
super().__init__(**kwargs)
self.num_patch = num_patch
self.proj = layers.Dense(embed_dim)
self.pos_embed = layers.Embedding(input_dim=num_patch, output_dim=embed_dim)
def call(self, patch):
pos = ops.arange(start=0, stop=self.num_patch)
return self.proj(patch) + self.pos_embed(pos)
class PatchMerging(keras.layers.Layer):
def __init__(self, num_patch, embed_dim):
super().__init__()
self.num_patch = num_patch
self.embed_dim = embed_dim
self.linear_trans = layers.Dense(2 * embed_dim, use_bias=False)
def call(self, x):
height, width = self.num_patch
_, _, C = x.shape
x = ops.reshape(x, (-1, height, width, C))
x0 = x[:, 0::2, 0::2, :]
x1 = x[:, 1::2, 0::2, :]
x2 = x[:, 0::2, 1::2, :]
x3 = x[:, 1::2, 1::2, :]
x = ops.concatenate((x0, x1, x2, x3), axis=-1)
x = ops.reshape(x, (-1, (height // 2) * (width // 2), 4 * C))
return self.linear_trans(x)tf.data.Dataset 준비
모든 단계를 트레이닝 가능한 가중치가 없는 tf.data로 수행합니다. 트레이닝, 검증, 테스트 세트를 준비합니다.
def augment(x):
x = tf.image.random_crop(x, size=(image_dimension, image_dimension, 3))
x = tf.image.random_flip_left_right(x)
return x
dataset = (
tf.data.Dataset.from_tensor_slices((x_train, y_train))
.map(lambda x, y: (augment(x), y))
.batch(batch_size=batch_size)
.map(lambda x, y: (patch_extract(x), y))
.prefetch(tf.data.experimental.AUTOTUNE)
)
dataset_val = (
tf.data.Dataset.from_tensor_slices((x_val, y_val))
.batch(batch_size=batch_size)
.map(lambda x, y: (patch_extract(x), y))
.prefetch(tf.data.experimental.AUTOTUNE)
)
dataset_test = (
tf.data.Dataset.from_tensor_slices((x_test, y_test))
.batch(batch_size=batch_size)
.map(lambda x, y: (patch_extract(x), y))
.prefetch(tf.data.experimental.AUTOTUNE)
)모델 빌드
이제 Swin Transformer 모델로 합쳐봅시다.
input = layers.Input(shape=(256, 12))
x = PatchEmbedding(num_patch_x * num_patch_y, embed_dim)(input)
x = SwinTransformer(
dim=embed_dim,
num_patch=(num_patch_x, num_patch_y),
num_heads=num_heads,
window_size=window_size,
shift_size=0,
num_mlp=num_mlp,
qkv_bias=qkv_bias,
dropout_rate=dropout_rate,
)(x)
x = SwinTransformer(
dim=embed_dim,
num_patch=(num_patch_x, num_patch_y),
num_heads=num_heads,
window_size=window_size,
shift_size=shift_size,
num_mlp=num_mlp,
qkv_bias=qkv_bias,
dropout_rate=dropout_rate,
)(x)
x = PatchMerging((num_patch_x, num_patch_y), embed_dim=embed_dim)(x)
x = layers.GlobalAveragePooling1D()(x)
output = layers.Dense(num_classes, activation="softmax")(x)결과
An NVIDIA GPU may be present on this machine, but a CUDA-enabled jaxlib is not installed. Falling back to cpu.CIFAR-100에 대해 트레이닝
우리는 CIFAR-100에 대해 모델을 트레이닝합니다. 여기에서는, 트레이닝 시간을 짧게 유지하기 위해 40 에포크 동안만 모델을 트레이닝합니다. 실제로, 수렴에 도달하려면 150 에포크 정도로 트레이닝해야 합니다.
model = keras.Model(input, output)
model.compile(
loss=keras.losses.CategoricalCrossentropy(label_smoothing=label_smoothing),
optimizer=keras.optimizers.AdamW(
learning_rate=learning_rate, weight_decay=weight_decay
),
metrics=[
keras.metrics.CategoricalAccuracy(name="accuracy"),
keras.metrics.TopKCategoricalAccuracy(5, name="top-5-accuracy"),
],
)
history = model.fit(
dataset,
batch_size=batch_size,
epochs=num_epochs,
validation_data=dataset_val,
)결과
Epoch 1/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 644s 2s/step - accuracy: 0.0517 - loss: 4.3948 - top-5-accuracy: 0.1816 - val_accuracy: 0.1396 - val_loss: 3.7930 - val_top-5-accuracy: 0.3922
Epoch 2/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 626s 2s/step - accuracy: 0.1606 - loss: 3.7267 - top-5-accuracy: 0.4209 - val_accuracy: 0.1946 - val_loss: 3.5560 - val_top-5-accuracy: 0.4862
Epoch 3/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 634s 2s/step - accuracy: 0.2160 - loss: 3.4910 - top-5-accuracy: 0.5076 - val_accuracy: 0.2440 - val_loss: 3.3946 - val_top-5-accuracy: 0.5384
Epoch 4/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 620s 2s/step - accuracy: 0.2599 - loss: 3.3266 - top-5-accuracy: 0.5628 - val_accuracy: 0.2730 - val_loss: 3.2732 - val_top-5-accuracy: 0.5812
Epoch 5/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 634s 2s/step - accuracy: 0.2841 - loss: 3.2082 - top-5-accuracy: 0.5988 - val_accuracy: 0.2878 - val_loss: 3.1837 - val_top-5-accuracy: 0.6050
Epoch 6/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 617s 2s/step - accuracy: 0.3049 - loss: 3.1199 - top-5-accuracy: 0.6262 - val_accuracy: 0.3110 - val_loss: 3.0970 - val_top-5-accuracy: 0.6292
Epoch 7/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 620s 2s/step - accuracy: 0.3271 - loss: 3.0387 - top-5-accuracy: 0.6501 - val_accuracy: 0.3292 - val_loss: 3.0374 - val_top-5-accuracy: 0.6488
Epoch 8/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 615s 2s/step - accuracy: 0.3454 - loss: 2.9764 - top-5-accuracy: 0.6679 - val_accuracy: 0.3480 - val_loss: 2.9921 - val_top-5-accuracy: 0.6598
Epoch 9/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 617s 2s/step - accuracy: 0.3571 - loss: 2.9272 - top-5-accuracy: 0.6801 - val_accuracy: 0.3522 - val_loss: 2.9585 - val_top-5-accuracy: 0.6746
Epoch 10/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 624s 2s/step - accuracy: 0.3658 - loss: 2.8809 - top-5-accuracy: 0.6924 - val_accuracy: 0.3562 - val_loss: 2.9364 - val_top-5-accuracy: 0.6784
Epoch 11/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 634s 2s/step - accuracy: 0.3796 - loss: 2.8425 - top-5-accuracy: 0.7021 - val_accuracy: 0.3654 - val_loss: 2.9100 - val_top-5-accuracy: 0.6832
Epoch 12/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 622s 2s/step - accuracy: 0.3884 - loss: 2.8113 - top-5-accuracy: 0.7103 - val_accuracy: 0.3740 - val_loss: 2.8808 - val_top-5-accuracy: 0.6948
Epoch 13/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 621s 2s/step - accuracy: 0.3994 - loss: 2.7718 - top-5-accuracy: 0.7239 - val_accuracy: 0.3778 - val_loss: 2.8637 - val_top-5-accuracy: 0.6994
Epoch 14/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 634s 2s/step - accuracy: 0.4072 - loss: 2.7491 - top-5-accuracy: 0.7271 - val_accuracy: 0.3848 - val_loss: 2.8533 - val_top-5-accuracy: 0.7002
Epoch 15/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 614s 2s/step - accuracy: 0.4142 - loss: 2.7180 - top-5-accuracy: 0.7344 - val_accuracy: 0.3880 - val_loss: 2.8383 - val_top-5-accuracy: 0.7080
Epoch 16/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 614s 2s/step - accuracy: 0.4231 - loss: 2.6918 - top-5-accuracy: 0.7392 - val_accuracy: 0.3934 - val_loss: 2.8323 - val_top-5-accuracy: 0.7072
Epoch 17/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 617s 2s/step - accuracy: 0.4339 - loss: 2.6633 - top-5-accuracy: 0.7484 - val_accuracy: 0.3972 - val_loss: 2.8237 - val_top-5-accuracy: 0.7138
Epoch 18/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 617s 2s/step - accuracy: 0.4388 - loss: 2.6436 - top-5-accuracy: 0.7506 - val_accuracy: 0.3984 - val_loss: 2.8119 - val_top-5-accuracy: 0.7144
Epoch 19/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 610s 2s/step - accuracy: 0.4439 - loss: 2.6251 - top-5-accuracy: 0.7552 - val_accuracy: 0.4020 - val_loss: 2.8044 - val_top-5-accuracy: 0.7178
Epoch 20/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 611s 2s/step - accuracy: 0.4540 - loss: 2.5989 - top-5-accuracy: 0.7652 - val_accuracy: 0.4012 - val_loss: 2.7969 - val_top-5-accuracy: 0.7246
Epoch 21/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 618s 2s/step - accuracy: 0.4586 - loss: 2.5760 - top-5-accuracy: 0.7684 - val_accuracy: 0.4092 - val_loss: 2.7807 - val_top-5-accuracy: 0.7254
Epoch 22/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 618s 2s/step - accuracy: 0.4607 - loss: 2.5624 - top-5-accuracy: 0.7724 - val_accuracy: 0.4158 - val_loss: 2.7721 - val_top-5-accuracy: 0.7232
Epoch 23/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 634s 2s/step - accuracy: 0.4658 - loss: 2.5407 - top-5-accuracy: 0.7786 - val_accuracy: 0.4180 - val_loss: 2.7767 - val_top-5-accuracy: 0.7280
Epoch 24/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 617s 2s/step - accuracy: 0.4744 - loss: 2.5233 - top-5-accuracy: 0.7840 - val_accuracy: 0.4164 - val_loss: 2.7707 - val_top-5-accuracy: 0.7300
Epoch 25/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 615s 2s/step - accuracy: 0.4758 - loss: 2.5129 - top-5-accuracy: 0.7847 - val_accuracy: 0.4196 - val_loss: 2.7677 - val_top-5-accuracy: 0.7294
Epoch 26/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 610s 2s/step - accuracy: 0.4853 - loss: 2.4954 - top-5-accuracy: 0.7863 - val_accuracy: 0.4188 - val_loss: 2.7571 - val_top-5-accuracy: 0.7362
Epoch 27/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 610s 2s/step - accuracy: 0.4858 - loss: 2.4785 - top-5-accuracy: 0.7928 - val_accuracy: 0.4186 - val_loss: 2.7615 - val_top-5-accuracy: 0.7348
Epoch 28/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 613s 2s/step - accuracy: 0.4889 - loss: 2.4691 - top-5-accuracy: 0.7945 - val_accuracy: 0.4208 - val_loss: 2.7561 - val_top-5-accuracy: 0.7350
Epoch 29/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 634s 2s/step - accuracy: 0.4940 - loss: 2.4592 - top-5-accuracy: 0.7992 - val_accuracy: 0.4244 - val_loss: 2.7546 - val_top-5-accuracy: 0.7398
Epoch 30/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 634s 2s/step - accuracy: 0.4989 - loss: 2.4391 - top-5-accuracy: 0.8025 - val_accuracy: 0.4180 - val_loss: 2.7861 - val_top-5-accuracy: 0.7302
Epoch 31/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 610s 2s/step - accuracy: 0.4994 - loss: 2.4354 - top-5-accuracy: 0.8032 - val_accuracy: 0.4264 - val_loss: 2.7608 - val_top-5-accuracy: 0.7394
Epoch 32/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 607s 2s/step - accuracy: 0.5011 - loss: 2.4238 - top-5-accuracy: 0.8090 - val_accuracy: 0.4292 - val_loss: 2.7625 - val_top-5-accuracy: 0.7384
Epoch 33/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 634s 2s/step - accuracy: 0.5065 - loss: 2.4144 - top-5-accuracy: 0.8085 - val_accuracy: 0.4288 - val_loss: 2.7517 - val_top-5-accuracy: 0.7328
Epoch 34/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 612s 2s/step - accuracy: 0.5094 - loss: 2.4099 - top-5-accuracy: 0.8093 - val_accuracy: 0.4260 - val_loss: 2.7550 - val_top-5-accuracy: 0.7390
Epoch 35/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 612s 2s/step - accuracy: 0.5109 - loss: 2.3980 - top-5-accuracy: 0.8115 - val_accuracy: 0.4278 - val_loss: 2.7496 - val_top-5-accuracy: 0.7396
Epoch 36/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 615s 2s/step - accuracy: 0.5178 - loss: 2.3868 - top-5-accuracy: 0.8139 - val_accuracy: 0.4296 - val_loss: 2.7519 - val_top-5-accuracy: 0.7404
Epoch 37/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 618s 2s/step - accuracy: 0.5151 - loss: 2.3842 - top-5-accuracy: 0.8150 - val_accuracy: 0.4308 - val_loss: 2.7504 - val_top-5-accuracy: 0.7424
Epoch 38/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 613s 2s/step - accuracy: 0.5169 - loss: 2.3798 - top-5-accuracy: 0.8159 - val_accuracy: 0.4360 - val_loss: 2.7522 - val_top-5-accuracy: 0.7464
Epoch 39/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 618s 2s/step - accuracy: 0.5228 - loss: 2.3641 - top-5-accuracy: 0.8201 - val_accuracy: 0.4374 - val_loss: 2.7386 - val_top-5-accuracy: 0.7452
Epoch 40/40
352/352 ━━━━━━━━━━━━━━━━━━━━ 634s 2s/step - accuracy: 0.5232 - loss: 2.3633 - top-5-accuracy: 0.8212 - val_accuracy: 0.4266 - val_loss: 2.7614 - val_top-5-accuracy: 0.7410모델의 트레이닝 진행 상황을 시각화해 보겠습니다.
plt.plot(history.history["loss"], label="train_loss")
plt.plot(history.history["val_loss"], label="val_loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.title("Train and Validation Losses Over Epochs", fontsize=14)
plt.legend()
plt.grid()
plt.show()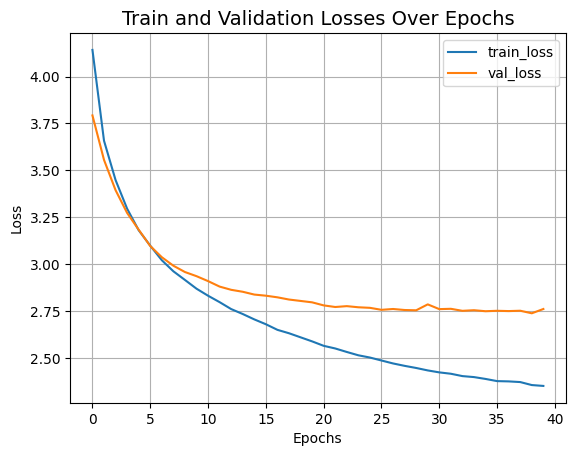
CIFAR-100에 대한 트레이닝의 최종 결과를 표시해 보겠습니다.
loss, accuracy, top_5_accuracy = model.evaluate(dataset_test)
print(f"Test loss: {round(loss, 2)}")
print(f"Test accuracy: {round(accuracy * 100, 2)}%")
print(f"Test top 5 accuracy: {round(top_5_accuracy * 100, 2)}%")결과
79/79 ━━━━━━━━━━━━━━━━━━━━ 26s 325ms/step - accuracy: 0.4474 - loss: 2.7119 - top-5-accuracy: 0.7556
Test loss: 2.7
Test accuracy: 44.8%
Test top 5 accuracy: 75.23%방금 트레이닝한 Swin Transformer 모델에는 152K개의 매개변수가 있으며, 위 그래프에서 볼 수 있듯이 과적합 징후 없이 단 40 에포크에서 top-5개 정확도를 최대 75% 테스트할 수 있습니다. 이는 우리가 이 네트워크를 더 오랫동안 트레이닝하고(아마도 좀 더 정규화와 함께) 훨씬 더 나은 성능을 얻을 수 있음을 의미합니다. 이 성능은 코사인 감쇠 학습률 스케쥴, 기타 데이터 보강 기술과 같은 추가적인 기술을 통해 더욱 향상될 수 있습니다. 실험하는 동안, 저는 스크린샷에서 볼 수 있듯이, 약간 더 높은 드롭아웃과 더 큰 임베딩 차원을 사용하여 150 에포크 동안 모델을 트레이닝하여, CIFAR-100에 대해 성능을 최대 72% 테스트 정확도로 끌어올려 보았습니다.
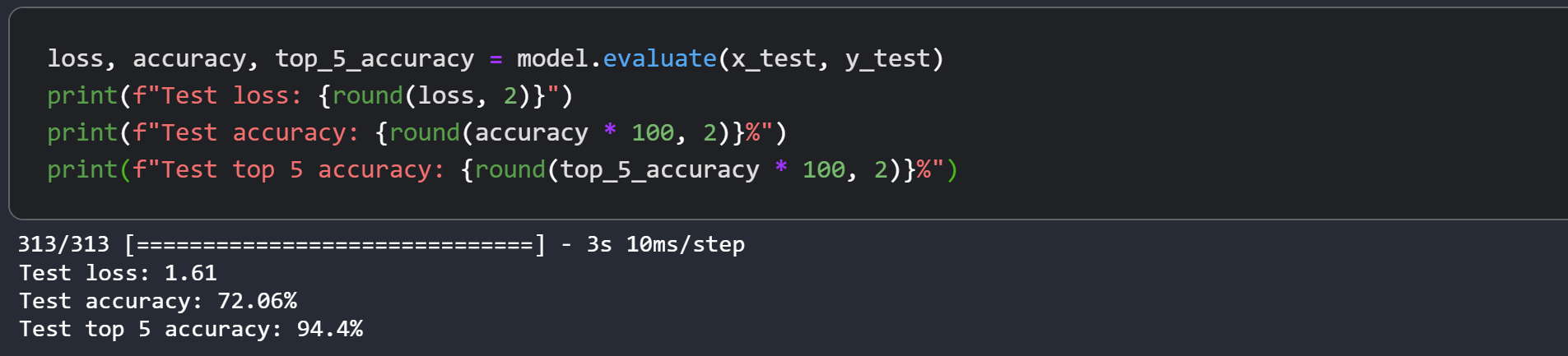
저자는 ImageNet에 대해 87.3%의 top-1 정확도를 제시합니다. 저자는 또한 입력 크기, 옵티마이저 등이 이 모델의 최종 성능에 어떤 영향을 미치는지 연구하기 위해 여러 가지 실험을 제시합니다. 저자는 객체 감지, 시맨틱 세그멘테이션 및 인스턴스 세그멘테이션에도 이 모델을 사용하는 방법을 제시하고, 이에 대한 경쟁력 있는 결과를 보고합니다. 원본 논문도 확인해 보시기 바랍니다.
이 예는 공식 PyTorch 및 TensorFlow 구현에서 영감을 얻었습니다.