Involutional 신경망

원본 링크 : https://keras.io/examples/vision/involution/
최종 확인 : 2024-11-20

저자 : Aritra Roy Gosthipaty
생성일 : 2021/07/25
최종 편집일 : 2021/07/25
설명 : 위치별 및 채널에 구애받지 않는(location-specific and channel-agnostic) “인볼루션(involution)” 커널에 대해 자세히 알아봅니다.

ⓘ 이 예제는 Keras 3를 사용합니다.

Colab

GitHub

소개

컨볼루션은 대부분의 최신 컴퓨터 비전을 위한 신경망의 기반이 되었습니다. 컨볼루션 커널은 공간에 구애받지 않고(spatial-agnostic) 채널에 따라(channel-specific) 달라집니다. 따라서, 공간적 위치에 따라 다른 시각적 패턴에 적응할 수 없습니다. 위치 관련 문제와 함께, 컨볼루션의 수용 영역은 장거리 공간 상호 작용을 캡처하는 데 어려움을 겪습니다.

위의 문제를 해결하기 위해, Li et. al.은 Involution: 시각 인식을 위한 컨볼루션의 내재적 반전(Inverting the Inherence of Convolution for VisualRecognition)에서 컨볼루션의 속성을 재고합니다. 저자들은 위치 특정적이고 채널에 구애받지 않는(location-specific and channel-agnostic) “인볼루션 커널(involution kernel)“을 제안합니다. 저자들은 연산의 위치 특정적(location-specific) 특성으로 인해, 셀프 어텐션이 인볼루션의 설계 패러다임에 해당한다고 말합니다.

이 예에서는 인볼루션 커널에 대해 설명하고, 컨볼루션과 인볼루션을 사용한 두 가지 이미지 분류 모델을 비교하며, 셀프 어텐션 레이어와 유사하게 그려봅니다.

셋업

import os

os.environ["KERAS_BACKEND"] = "tensorflow"

import tensorflow as tf
import keras
import matplotlib.pyplot as plt

# 재현성을 위해 시드를 설정합니다.
tf.random.set_seed(42)

컨볼루션

컨볼루션은 컴퓨터 비전을 위한 심층 신경망의 주축을 이루고 있습니다. 인볼루션을 이해하려면, 컨볼루션 연산에 대해 이야기할 필요가 있습니다.

png

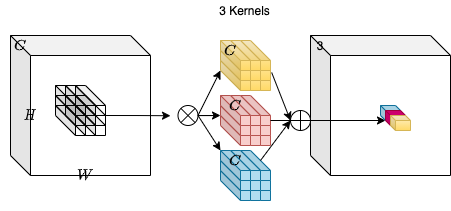
차원이 H, W, C_in인 입력 텐서 X를 생각해 봅시다. 우리는 각각 K, K, C_in 형태의 C_out 컨볼루션 커널의 모음을 취합니다. 입력 텐서와 커널 사이의 곱하기 덧셈 연산(multiply-add operation)을 통해, H, W, C_out 차원의 출력 텐서 Y를 얻습니다.

위의 다이어그램에서 C_out=3입니다. 이렇게 하면 H, W, 3 형태의 출력 텐서가 됩니다. 컨볼루션 커널은 입력 텐서의 공간적 위치에 의존하지 않기 때문에, 위치 불가지론적(location-agnostic) 이라는 것을 알 수 있습니다. 반면, 출력 텐서의 각 채널은 특정 컨볼루션 필터를 기반으로 하므로 채널별(channel-specific) 입니다.

인볼루션

이 아이디어는 위치에 따라 달라지는(location-specific) 작업과 채널에 구애받지 않는(channel-agnostic) 작업을 모두 구현하는 것입니다. 이러한 특정 속성을 구현하는 데는 어려움이 있습니다. (각 공간 위치에 대해) 고정된 수의 인볼루션 커널을 사용하면, 가변 해상도 입력 텐서를 처리할 수 없게 됩니다.

이 문제를 해결하기 위해, 저자들은 특정 공간 위치에 따라 각 커널을 생성 하는 방법을 고려했습니다. 이 방법을 사용하면, 가변 해상도 입력 텐서를 쉽게 처리할 수 있을 것입니다. 아래 다이어그램은 이 커널 생성 방법에 대한 직관을 제공합니다.

png

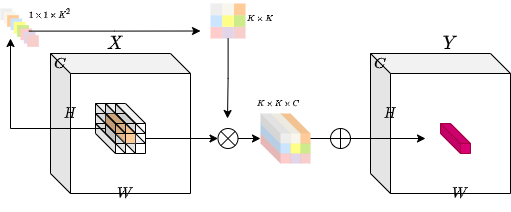
class Involution(keras.layers.Layer):
    def __init__(
        self, channel, group_number, kernel_size, stride, reduction_ratio, name
    ):
        super().__init__(name=name)

        # 매개 변수를 초기화.
        self.channel = channel
        self.group_number = group_number
        self.kernel_size = kernel_size
        self.stride = stride
        self.reduction_ratio = reduction_ratio

    def build(self, input_shape):
        # 입력의 모양을 가져오기.
        (_, height, width, num_channels) = input_shape

        # 보폭(strides)에 따라 높이와 너비를 조정.
        height = height // self.stride
        width = width // self.stride

        # 스트라이드가 1보다 큰 경우, 입력 텐서를 평균 풀링하는 레이어를 정의.
        self.stride_layer = (
            keras.layers.AveragePooling2D(
                pool_size=self.stride, strides=self.stride, padding="same"
            )
            if self.stride > 1
            else tf.identity
        )
        # 커널 생성 레이어를 정의.
        self.kernel_gen = keras.Sequential(
            [
                keras.layers.Conv2D(
                    filters=self.channel // self.reduction_ratio, kernel_size=1
                ),
                keras.layers.BatchNormalization(),
                keras.layers.ReLU(),
                keras.layers.Conv2D(
                    filters=self.kernel_size * self.kernel_size * self.group_number,
                    kernel_size=1,
                ),
            ]
        )
        # reshape 레이어 정의
        self.kernel_reshape = keras.layers.Reshape(
            target_shape=(
                height,
                width,
                self.kernel_size * self.kernel_size,
                1,
                self.group_number,
            )
        )
        self.input_patches_reshape = keras.layers.Reshape(
            target_shape=(
                height,
                width,
                self.kernel_size * self.kernel_size,
                num_channels // self.group_number,
                self.group_number,
            )
        )
        self.output_reshape = keras.layers.Reshape(
            target_shape=(height, width, num_channels)
        )

    def call(self, x):
        # 입력 텐서를 기준으로 커널을 생성.
        # B, H, W, K*K*G
        kernel_input = self.stride_layer(x)
        kernel = self.kernel_gen(kernel_input)

        # 커널 reshape
        # B, H, W, K*K, 1, G
        kernel = self.kernel_reshape(kernel)

        # 입력 패치 추출.
        # B, H, W, K*K*C
        input_patches = tf.image.extract_patches(
            images=x,
            sizes=[1, self.kernel_size, self.kernel_size, 1],
            strides=[1, self.stride, self.stride, 1],
            rates=[1, 1, 1, 1],
            padding="SAME",
        )

        # 이후 연산에 맞게 입력 패치를 reshape.
        # B, H, W, K*K, C//G, G
        input_patches = self.input_patches_reshape(input_patches)

        # 커널과 패치의 곱하기 덧셈(multiply-add) 연산을 계산.
        # B, H, W, K*K, C//G, G
        output = tf.multiply(kernel, input_patches)
        # B, H, W, C//G, G
        output = tf.reduce_sum(output, axis=3)

        # 출력 커널 Reshape.
        # B, H, W, C
        output = self.output_reshape(output)

        # 출력 텐서와 커널을 반환.
        return output, kernel

인볼루션 레이어 테스트하기

# 입력 텐서를 정의.
input_tensor = tf.random.normal((32, 256, 256, 3))

# 스트라이드 1로 인볼루션을 계산.
output_tensor, _ = Involution(
    channel=3, group_number=1, kernel_size=5, stride=1, reduction_ratio=1, name="inv_1"
)(input_tensor)
print(f"with stride 1 ouput shape: {output_tensor.shape}")

# 스트라이드 2로 인볼루션을 계산.
output_tensor, _ = Involution(
    channel=3, group_number=1, kernel_size=5, stride=2, reduction_ratio=1, name="inv_2"
)(input_tensor)
print(f"with stride 2 ouput shape: {output_tensor.shape}")

# 스트라이드 1, 채널 16, reduction ratio 2로 인볼루션을 계산.
output_tensor, _ = Involution(
    channel=16, group_number=1, kernel_size=5, stride=1, reduction_ratio=2, name="inv_3"
)(input_tensor)
print(
    "with channel 16 and reduction ratio 2 ouput shape: {}".format(output_tensor.shape)
)

결과

with stride 1 ouput shape: (32, 256, 256, 3)
with stride 2 ouput shape: (32, 128, 128, 3)
with channel 16 and reduction ratio 2 ouput shape: (32, 256, 256, 3)

이미지 분류

이 섹션에서는, 이미지 분류기 모델을 빌드하겠습니다. 컨볼루션을 사용하는 모델과 인볼루션을 사용하는 모델 두 가지를 만들 것입니다.

이미지 분류 모델은 Google의 컨볼루션 신경망(CNN) 튜토리얼에서 많은 영감을 받았습니다.

CIFAR10 데이터세트 얻기

# CIFAR10 데이터세트 로드.
print("loading the CIFAR10 dataset...")
(
    (train_images, train_labels),
    (
        test_images,
        test_labels,
    ),
) = keras.datasets.cifar10.load_data()

# 픽셀 값을 0에서 1 사이로 정규화.
(train_images, test_images) = (train_images / 255.0, test_images / 255.0)

# 데이터 세트를 셔플하고 배치화.
train_ds = (
    tf.data.Dataset.from_tensor_slices((train_images, train_labels))
    .shuffle(256)
    .batch(256)
)
test_ds = tf.data.Dataset.from_tensor_slices((test_images, test_labels)).batch(256)

결과

loading the CIFAR10 dataset...

데이터 시각화

class_names = [
    "airplane",
    "automobile",
    "bird",
    "cat",
    "deer",
    "dog",
    "frog",
    "horse",
    "ship",
    "truck",
]

plt.figure(figsize=(10, 10))
for i in range(25):
    plt.subplot(5, 5, i + 1)
    plt.xticks([])
    plt.yticks([])
    plt.grid(False)
    plt.imshow(train_images[i])
    plt.xlabel(class_names[train_labels[i][0]])
plt.show()

png

컨볼루션 신경망

# conv 모델 빌드.
print("building the convolution model...")
conv_model = keras.Sequential(
    [
        keras.layers.Conv2D(32, (3, 3), input_shape=(32, 32, 3), padding="same"),
        keras.layers.ReLU(name="relu1"),
        keras.layers.MaxPooling2D((2, 2)),
        keras.layers.Conv2D(64, (3, 3), padding="same"),
        keras.layers.ReLU(name="relu2"),
        keras.layers.MaxPooling2D((2, 2)),
        keras.layers.Conv2D(64, (3, 3), padding="same"),
        keras.layers.ReLU(name="relu3"),
        keras.layers.Flatten(),
        keras.layers.Dense(64, activation="relu"),
        keras.layers.Dense(10),
    ]
)

# 필요한 손실 함수 및 옵티마이저를 사용하여 모델을 컴파일.
print("compiling the convolution model...")
conv_model.compile(
    optimizer="adam",
    loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
    metrics=["accuracy"],
)

# 모델 트레이닝.
print("conv model training...")
conv_hist = conv_model.fit(train_ds, epochs=20, validation_data=test_ds)

결과

building the convolution model...
compiling the convolution model...
conv model training...
Epoch 1/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 6s 15ms/step - accuracy: 0.3068 - loss: 1.9000 - val_accuracy: 0.4861 - val_loss: 1.4593
Epoch 2/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.5153 - loss: 1.3603 - val_accuracy: 0.5741 - val_loss: 1.1913
Epoch 3/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.5949 - loss: 1.1517 - val_accuracy: 0.6095 - val_loss: 1.0965
Epoch 4/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6414 - loss: 1.0330 - val_accuracy: 0.6260 - val_loss: 1.0635
Epoch 5/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6690 - loss: 0.9485 - val_accuracy: 0.6622 - val_loss: 0.9833
Epoch 6/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.6951 - loss: 0.8764 - val_accuracy: 0.6783 - val_loss: 0.9413
Epoch 7/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.7122 - loss: 0.8167 - val_accuracy: 0.6856 - val_loss: 0.9134
Epoch 8/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.7299 - loss: 0.7709 - val_accuracy: 0.7001 - val_loss: 0.8792
Epoch 9/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.7467 - loss: 0.7288 - val_accuracy: 0.6992 - val_loss: 0.8821
Epoch 10/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.7591 - loss: 0.6982 - val_accuracy: 0.7235 - val_loss: 0.8237
Epoch 11/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.7725 - loss: 0.6550 - val_accuracy: 0.7115 - val_loss: 0.8521
Epoch 12/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.7808 - loss: 0.6302 - val_accuracy: 0.7051 - val_loss: 0.8823
Epoch 13/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.7860 - loss: 0.6101 - val_accuracy: 0.7122 - val_loss: 0.8635
Epoch 14/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.7998 - loss: 0.5786 - val_accuracy: 0.7214 - val_loss: 0.8348
Epoch 15/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8117 - loss: 0.5473 - val_accuracy: 0.7139 - val_loss: 0.8835
Epoch 16/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8168 - loss: 0.5267 - val_accuracy: 0.7155 - val_loss: 0.8840
Epoch 17/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8266 - loss: 0.5022 - val_accuracy: 0.7239 - val_loss: 0.8576
Epoch 18/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8374 - loss: 0.4750 - val_accuracy: 0.7262 - val_loss: 0.8756
Epoch 19/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.8452 - loss: 0.4505 - val_accuracy: 0.7235 - val_loss: 0.9049
Epoch 20/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.8531 - loss: 0.4283 - val_accuracy: 0.7304 - val_loss: 0.8962

인볼루션 신경망

# 인볼루션 모델을 빌드.
print("building the involution model...")

inputs = keras.Input(shape=(32, 32, 3))
x, _ = Involution(
    channel=3, group_number=1, kernel_size=3, stride=1, reduction_ratio=2, name="inv_1"
)(inputs)
x = keras.layers.ReLU()(x)
x = keras.layers.MaxPooling2D((2, 2))(x)
x, _ = Involution(
    channel=3, group_number=1, kernel_size=3, stride=1, reduction_ratio=2, name="inv_2"
)(x)
x = keras.layers.ReLU()(x)
x = keras.layers.MaxPooling2D((2, 2))(x)
x, _ = Involution(
    channel=3, group_number=1, kernel_size=3, stride=1, reduction_ratio=2, name="inv_3"
)(x)
x = keras.layers.ReLU()(x)
x = keras.layers.Flatten()(x)
x = keras.layers.Dense(64, activation="relu")(x)
outputs = keras.layers.Dense(10)(x)

inv_model = keras.Model(inputs=[inputs], outputs=[outputs], name="inv_model")

# 필요한 손실 함수 및 옵티마이저를 사용하여 모델을 컴파일.
print("compiling the involution model...")
inv_model.compile(
    optimizer="adam",
    loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
    metrics=["accuracy"],
)

# 모델 트레이닝
print("inv model training...")
inv_hist = inv_model.fit(train_ds, epochs=20, validation_data=test_ds)

결과

building the involution model...
compiling the involution model...
inv model training...
Epoch 1/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 9s 25ms/step - accuracy: 0.1369 - loss: 2.2728 - val_accuracy: 0.2716 - val_loss: 2.1041
Epoch 2/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.2922 - loss: 1.9489 - val_accuracy: 0.3478 - val_loss: 1.8275
Epoch 3/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.3477 - loss: 1.8098 - val_accuracy: 0.3782 - val_loss: 1.7435
Epoch 4/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.3741 - loss: 1.7420 - val_accuracy: 0.3901 - val_loss: 1.6943
Epoch 5/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.3931 - loss: 1.6942 - val_accuracy: 0.4007 - val_loss: 1.6639
Epoch 6/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.4057 - loss: 1.6622 - val_accuracy: 0.4108 - val_loss: 1.6494
Epoch 7/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4134 - loss: 1.6374 - val_accuracy: 0.4202 - val_loss: 1.6363
Epoch 8/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4200 - loss: 1.6166 - val_accuracy: 0.4312 - val_loss: 1.6062
Epoch 9/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.4286 - loss: 1.5949 - val_accuracy: 0.4316 - val_loss: 1.6018
Epoch 10/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.4346 - loss: 1.5794 - val_accuracy: 0.4346 - val_loss: 1.5963
Epoch 11/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4395 - loss: 1.5641 - val_accuracy: 0.4388 - val_loss: 1.5831
Epoch 12/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 5ms/step - accuracy: 0.4445 - loss: 1.5502 - val_accuracy: 0.4443 - val_loss: 1.5826
Epoch 13/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4493 - loss: 1.5391 - val_accuracy: 0.4497 - val_loss: 1.5574
Epoch 14/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4528 - loss: 1.5255 - val_accuracy: 0.4547 - val_loss: 1.5433
Epoch 15/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 4ms/step - accuracy: 0.4575 - loss: 1.5148 - val_accuracy: 0.4548 - val_loss: 1.5438
Epoch 16/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4599 - loss: 1.5072 - val_accuracy: 0.4581 - val_loss: 1.5323
Epoch 17/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4664 - loss: 1.4957 - val_accuracy: 0.4598 - val_loss: 1.5321
Epoch 18/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4701 - loss: 1.4863 - val_accuracy: 0.4575 - val_loss: 1.5302
Epoch 19/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4737 - loss: 1.4790 - val_accuracy: 0.4676 - val_loss: 1.5233
Epoch 20/20
 196/196 ━━━━━━━━━━━━━━━━━━━━ 1s 6ms/step - accuracy: 0.4771 - loss: 1.4740 - val_accuracy: 0.4719 - val_loss: 1.5096

비교

이 섹션에서는, 두 모델을 살펴보고 몇 가지 요점을 비교해 보겠습니다.

파라미터

비슷한 아키텍처의 경우, CNN의 파라미터가 INN(인볼루션 신경망)보다 훨씬 더 크다는 것을 알 수 있습니다.

conv_model.summary()

inv_model.summary()

결과

Model: "sequential_3"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape              ┃    Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━┩
│ conv2d_6 (Conv2D)               │ (None, 32, 32, 32)        │        896 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ relu1 (ReLU)                    │ (None, 32, 32, 32)        │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ max_pooling2d (MaxPooling2D)    │ (None, 16, 16, 32)        │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ conv2d_7 (Conv2D)               │ (None, 16, 16, 64)        │     18,496 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ relu2 (ReLU)                    │ (None, 16, 16, 64)        │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ max_pooling2d_1 (MaxPooling2D)  │ (None, 8, 8, 64)          │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ conv2d_8 (Conv2D)               │ (None, 8, 8, 64)          │     36,928 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ relu3 (ReLU)                    │ (None, 8, 8, 64)          │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ flatten (Flatten)               │ (None, 4096)              │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ dense (Dense)                   │ (None, 64)                │    262,208 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ dense_1 (Dense)                 │ (None, 10)                │        650 │
└─────────────────────────────────┴───────────────────────────┴────────────┘
 Total params: 957,536 (3.65 MB)
 Trainable params: 319,178 (1.22 MB)
 Non-trainable params: 0 (0.00 B)
 Optimizer params: 638,358 (2.44 MB)
Model: "inv_model"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┓
┃ Layer (type)                    ┃ Output Shape              ┃    Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━┩
│ input_layer_4 (InputLayer)      │ (None, 32, 32, 3)         │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ inv_1 (Involution)              │ [(None, 32, 32, 3),       │         26 │
│                                 │ (None, 32, 32, 9, 1, 1)]  │            │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ re_lu_4 (ReLU)                  │ (None, 32, 32, 3)         │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ max_pooling2d_2 (MaxPooling2D)  │ (None, 16, 16, 3)         │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ inv_2 (Involution)              │ [(None, 16, 16, 3),       │         26 │
│                                 │ (None, 16, 16, 9, 1, 1)]  │            │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ re_lu_6 (ReLU)                  │ (None, 16, 16, 3)         │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ max_pooling2d_3 (MaxPooling2D)  │ (None, 8, 8, 3)           │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ inv_3 (Involution)              │ [(None, 8, 8, 3), (None,  │         26 │
│                                 │ 8, 8, 9, 1, 1)]           │            │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ re_lu_8 (ReLU)                  │ (None, 8, 8, 3)           │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ flatten_1 (Flatten)             │ (None, 192)               │          0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ dense_2 (Dense)                 │ (None, 64)                │     12,352 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ dense_3 (Dense)                 │ (None, 10)                │        650 │
└─────────────────────────────────┴───────────────────────────┴────────────┘
 Total params: 39,230 (153.25 KB)
 Trainable params: 13,074 (51.07 KB)
 Non-trainable params: 6 (24.00 B)
 Optimizer params: 26,150 (102.15 KB)

손실 및 정확도 플롯

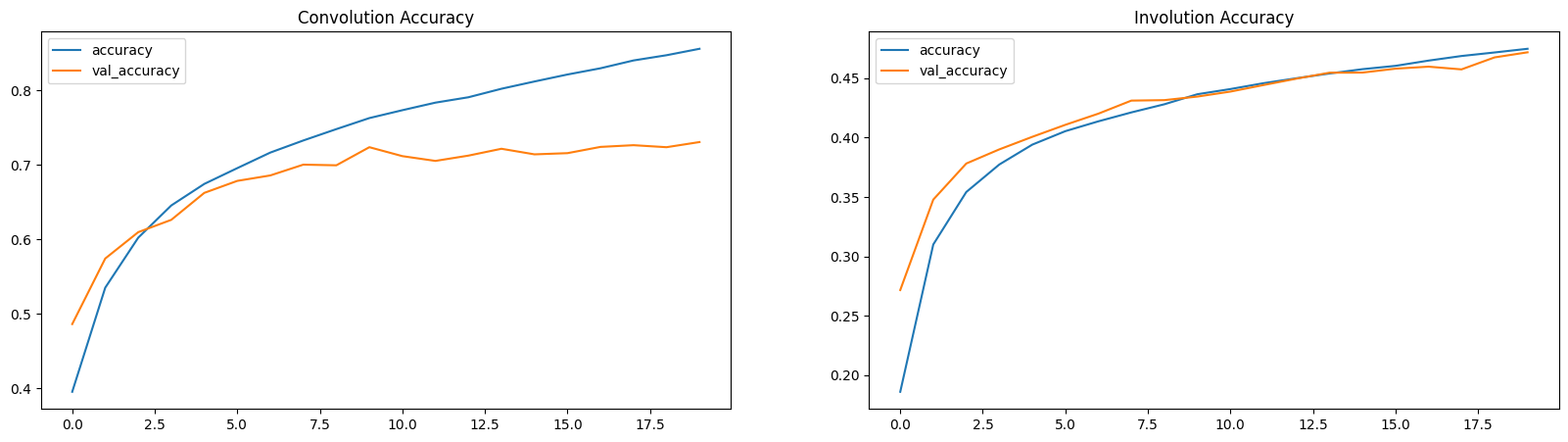
여기서, 손실 및 정확도 플롯은 INN이 (적은 매개변수로) 느린 학습자임을 보여줍니다.

plt.figure(figsize=(20, 5))

plt.subplot(1, 2, 1)
plt.title("Convolution Loss")
plt.plot(conv_hist.history["loss"], label="loss")
plt.plot(conv_hist.history["val_loss"], label="val_loss")
plt.legend()

plt.subplot(1, 2, 2)
plt.title("Involution Loss")
plt.plot(inv_hist.history["loss"], label="loss")
plt.plot(inv_hist.history["val_loss"], label="val_loss")
plt.legend()

plt.show()

plt.figure(figsize=(20, 5))

plt.subplot(1, 2, 1)
plt.title("Convolution Accuracy")
plt.plot(conv_hist.history["accuracy"], label="accuracy")
plt.plot(conv_hist.history["val_accuracy"], label="val_accuracy")
plt.legend()

plt.subplot(1, 2, 2)
plt.title("Involution Accuracy")
plt.plot(inv_hist.history["accuracy"], label="accuracy")
plt.plot(inv_hist.history["val_accuracy"], label="val_accuracy")
plt.legend()

plt.show()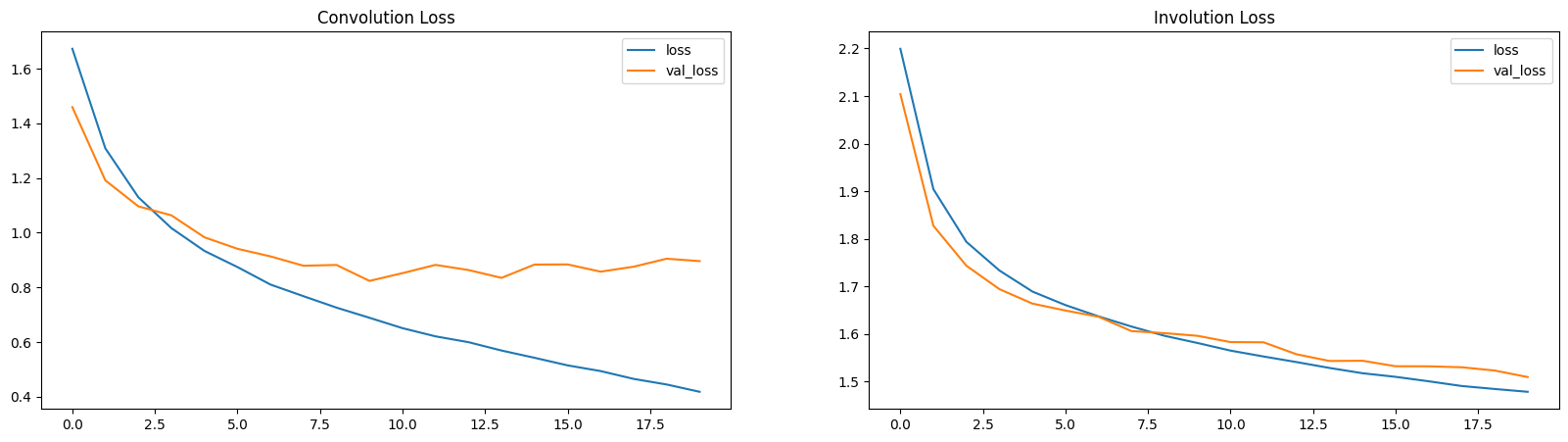

png

인볼루션 커널 시각화

커널을 시각화하기 위해, 각 인볼루션 커널에서 K×K 값의 합을 구합니다. 서로 다른 공간 위치에 있는 모든 대표자(representatives)가 해당 히트 맵의 프레임을 구성합니다.

저자들은 다음과 같이 언급합니다:

“우리가 제안한 인볼루션은 셀프 어텐션을 연상시키며, 본질적으로 그것의 일반화된 버전이 될 수 있습니다.”

커널을 시각화하면 실제로 이미지의 어텐션 맵을 얻을 수 있습니다. 학습된 인볼루션 커널은 입력 텐서의 개별 공간 위치에 대한 어텐션을 제공합니다. 위치 특정적(location-specific) 속성은 셀프 어텐션이 속하는 모델의 일반적 공간으로 인볼루션을 만듭니다.

layer_names = ["inv_1", "inv_2", "inv_3"]
outputs = [inv_model.get_layer(name).output[1] for name in layer_names]
vis_model = keras.Model(inv_model.input, outputs)

fig, axes = plt.subplots(nrows=10, ncols=4, figsize=(10, 30))

for ax, test_image in zip(axes, test_images[:10]):
    (inv1_kernel, inv2_kernel, inv3_kernel) = vis_model.predict(test_image[None, ...])
    inv1_kernel = tf.reduce_sum(inv1_kernel, axis=[-1, -2, -3])
    inv2_kernel = tf.reduce_sum(inv2_kernel, axis=[-1, -2, -3])
    inv3_kernel = tf.reduce_sum(inv3_kernel, axis=[-1, -2, -3])

    ax[0].imshow(keras.utils.array_to_img(test_image))
    ax[0].set_title("Input Image")

    ax[1].imshow(keras.utils.array_to_img(inv1_kernel[0, ..., None]))
    ax[1].set_title("Involution Kernel 1")

    ax[2].imshow(keras.utils.array_to_img(inv2_kernel[0, ..., None]))
    ax[2].set_title("Involution Kernel 2")

    ax[3].imshow(keras.utils.array_to_img(inv3_kernel[0, ..., None]))
    ax[3].set_title("Involution Kernel 3")

결과

 1/1 ━━━━━━━━━━━━━━━━━━━━ 1s 503ms/step
 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step
 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step
 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step
 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 11ms/step
 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step
 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step
 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step
 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 10ms/step
 1/1 ━━━━━━━━━━━━━━━━━━━━ 0s 9ms/step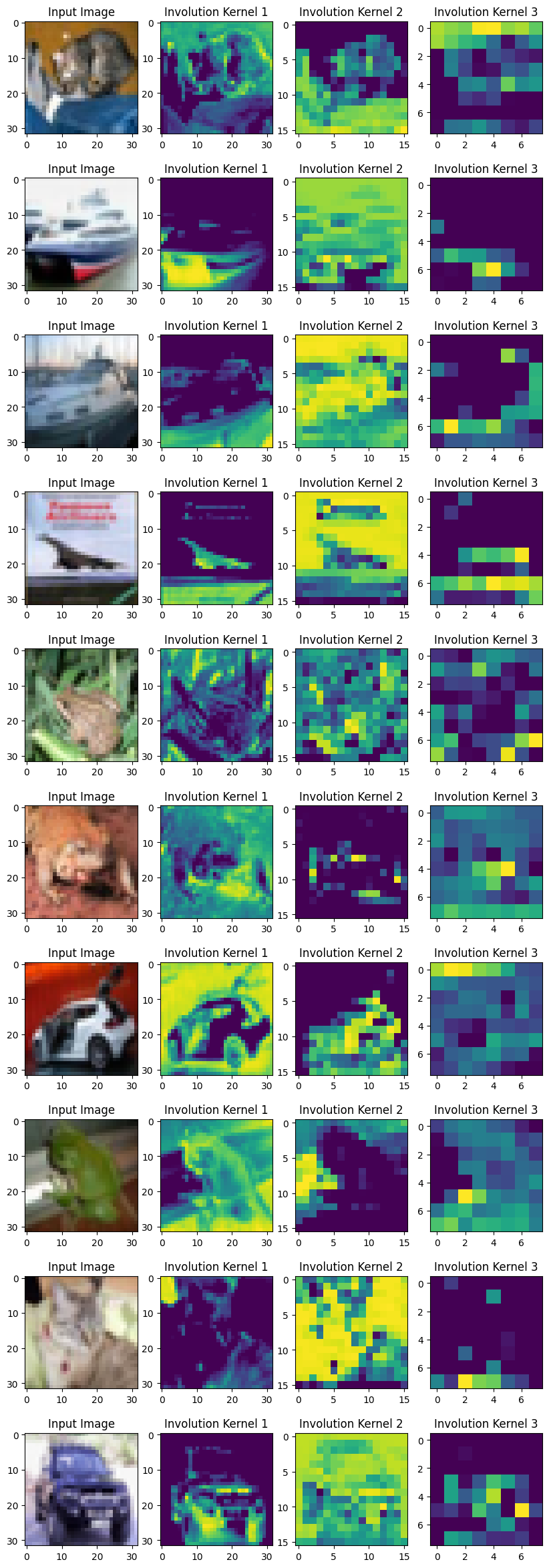

png

결론

이 예제에서는, 쉽게 재사용할 수 있는 Involution 레이어를 만드는 데 중점을 두었습니다. 특정 작업을 기준으로 비교했지만, 다른 작업에도 자유롭게 이 레이어를 사용해 결과를 보고해 보세요.

제가 보기에, 인볼루션의 핵심은 셀프 어텐션과의 관계입니다. 위치별(location-specific) 및 채널별(channel-spefic) 처리에 대한 직관은 많은 작업에서 의미가 있습니다.

다음을 학습함으로써, 앞으로 나아갈 수 있습니다:

인볼루션에 대한 Yannick의 동영상을 보면 더 잘 이해할 수 있습니다.
인볼루션 레이어의 다양한 하이퍼파라미터를 실험해 보세요.
인볼루션 레이어로 다양한 모델을 빌드해 보세요.
완전히 다른 커널 생성 방법을 시도하여 빌드해 보세요.

Hugging Face Hub에서 호스팅되는 트레이닝된 모델을 사용하고, Hugging Face Spaces에서 데모를 사용해 볼 수 있습니다.