컴팩트 컨볼루션 트랜스포머 (Compact Convolutional Transformers)
- 원본 링크 : https://keras.io/examples/vision/cct/
- 최종 확인 : 2024-11-20
저자 : Sayak Paul
생성일 : 2021/06/30
최종 편집일 : 2023/08/07
설명 : 효율적인 이미지 분류를 위한 컴팩트 컨볼루션 트랜스포머.
비전 트랜스포머(ViT) 논문에서 설명한 대로, 비전을 위한 트랜스포머 기반 아키텍처는 일반적으로 평소보다 더 큰 데이터세트와 더 긴 사전 트레이닝 스케쥴이 필요합니다. 약 백만 개의 이미지가 있는 ImageNet-1k는 ViT와 관련하여 중간 크기의 데이터 체제에 속하는 것으로 간주됩니다. 이는 주로 CNN과 달리, ViT(또는 일반적인 Transformer 기반 아키텍처)에는 (이미지 처리를 위한 컨볼루션과 같은) 귀납적 편향이 잘 알려져 있지 않기 때문입니다. 그렇다면 다음과 같은 질문이 생깁니다. 컨볼루션의 장점과 트랜스포머의 장점을 단일 네트워크 아키텍처에 결합할 수 없을까요? 이러한 이점에는 매개변수 효율성과 장거리 및 전역 종속성(이미지 내 여러 영역 간의 상호 작용)을 처리하기 위한 셀프 어텐션이 포함됩니다.
컴팩트 트랜스포머로 빅데이터 패러다임 탈출하기에서 Hassani et al.은 이를 위한 접근 방식을 제시합니다. 그들은 컴팩트 컨볼루션 트랜스포머(CCT) 아키텍처를 제안했습니다. 이 예제에서는, CCT를 구현하여 CIFAR-10 데이터 세트에 대해 얼마나 잘 작동하는지 살펴보겠습니다.
셀프 어텐션이나 트랜스포머의 개념이 생소하다면, François Chollet의 저서 파이썬으로 딥러닝하기(Deep Learning with Python) 에서 이 챕터을 읽어보실 수 있습니다. 이 예제에서는 다른 예제인 비전 트랜스포머로 이미지 분류의 코드 스니펫을 사용합니다.
Imports
from keras import layers
import keras
import matplotlib.pyplot as plt
import numpy as np하이퍼파라미터 및 상수
positional_emb = True
conv_layers = 2
projection_dim = 128
num_heads = 2
transformer_units = [
projection_dim,
projection_dim,
]
transformer_layers = 2
stochastic_depth_rate = 0.1
learning_rate = 0.001
weight_decay = 0.0001
batch_size = 128
num_epochs = 30
image_size = 32CIFAR-10 데이터세트 불러오기
num_classes = 10
input_shape = (32, 32, 3)
(x_train, y_train), (x_test, y_test) = keras.datasets.cifar10.load_data()
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
print(f"x_train shape: {x_train.shape} - y_train shape: {y_train.shape}")
print(f"x_test shape: {x_test.shape} - y_test shape: {y_test.shape}")결과
x_train shape: (50000, 32, 32, 3) - y_train shape: (50000, 10)
x_test shape: (10000, 32, 32, 3) - y_test shape: (10000, 10)CCT 토큰나이저
CCT 저자가 소개한 첫 번째 레시피는 이미지 처리를 위한 토큰화 도구(tokenizer)입니다. 표준 ViT에서는, 이미지가 균일한 중첩되지 않는 패치로 구성됩니다. 이렇게 하면 서로 다른 패치 사이에 존재하는 경계 레벨 정보가 제거됩니다. 이는 신경망이 지역 정보를 효과적으로 활용하기 위해 중요합니다. 아래 그림은 이미지를 패치로 구성하는 방법을 보여주는 그림입니다.

우리는 컨볼루션이 지역 정보를 활용하는데 매우 효과적이라는 것을 이미 알고 있습니다. 따라서, 저자는 이를 기반으로, 이미지 패치를 생성하기 위해 모든 컨볼루션 미니 네트워크를 도입합니다.
class CCTTokenizer(layers.Layer):
def __init__(
self,
kernel_size=3,
stride=1,
padding=1,
pooling_kernel_size=3,
pooling_stride=2,
num_conv_layers=conv_layers,
num_output_channels=[64, 128],
positional_emb=positional_emb,
**kwargs,
):
super().__init__(**kwargs)
# 이것이 우리의 토큰나이저입니다.
self.conv_model = keras.Sequential()
for i in range(num_conv_layers):
self.conv_model.add(
layers.Conv2D(
num_output_channels[i],
kernel_size,
stride,
padding="valid",
use_bias=False,
activation="relu",
kernel_initializer="he_normal",
)
)
self.conv_model.add(layers.ZeroPadding2D(padding))
self.conv_model.add(
layers.MaxPooling2D(pooling_kernel_size, pooling_stride, "same")
)
self.positional_emb = positional_emb
def call(self, images):
outputs = self.conv_model(images)
# 이미지를 미니 네트워크에 통과시킨 후, 공간 차원을 flatten 하여 시퀀스를 형성합니다.
reshaped = keras.ops.reshape(
outputs,
(
-1,
keras.ops.shape(outputs)[1] * keras.ops.shape(outputs)[2],
keras.ops.shape(outputs)[-1],
),
)
return reshaped위치 임베딩은 CCT에서 선택 사항입니다. 위치 임베딩을 사용하려면, 아래에 정의된 레이어를 사용하면 됩니다.
class PositionEmbedding(keras.layers.Layer):
def __init__(
self,
sequence_length,
initializer="glorot_uniform",
**kwargs,
):
super().__init__(**kwargs)
if sequence_length is None:
raise ValueError("`sequence_length` must be an Integer, received `None`.")
self.sequence_length = int(sequence_length)
self.initializer = keras.initializers.get(initializer)
def get_config(self):
config = super().get_config()
config.update(
{
"sequence_length": self.sequence_length,
"initializer": keras.initializers.serialize(self.initializer),
}
)
return config
def build(self, input_shape):
feature_size = input_shape[-1]
self.position_embeddings = self.add_weight(
name="embeddings",
shape=[self.sequence_length, feature_size],
initializer=self.initializer,
trainable=True,
)
super().build(input_shape)
def call(self, inputs, start_index=0):
shape = keras.ops.shape(inputs)
feature_length = shape[-1]
sequence_length = shape[-2]
# trim을 사용하여 입력 시퀀스의 길이와 일치하도록 길이를 조정할 수 있으며,
# 이는 레이어의 sequence_length보다 작을 수 있습니다.
position_embeddings = keras.ops.convert_to_tensor(self.position_embeddings)
position_embeddings = keras.ops.slice(
position_embeddings,
(start_index, 0),
(sequence_length, feature_length),
)
return keras.ops.broadcast_to(position_embeddings, shape)
def compute_output_shape(self, input_shape):
return input_shape시퀀스 풀링
CCT에 도입된 또 다른 방법은 어텐션 풀링 또는 시퀀스 풀링입니다. ViT에서는, 클래스 토큰에 해당하는 특성 맵만 풀링된 다음, 후속 분류 작업(또는 다른 다운스트림 작업)에 사용됩니다.
class SequencePooling(layers.Layer):
def __init__(self):
super().__init__()
self.attention = layers.Dense(1)
def call(self, x):
attention_weights = keras.ops.softmax(self.attention(x), axis=1)
attention_weights = keras.ops.transpose(attention_weights, axes=(0, 2, 1))
weighted_representation = keras.ops.matmul(attention_weights, x)
return keras.ops.squeeze(weighted_representation, -2)정규화를 위한 확률적 깊이(Stochastic depth)
확률적 깊이는 레이어 세트를 무작위로 드롭하는 정규화 기법입니다. 추론 시에는 레이어가 그대로 유지됩니다. 드롭아웃과 매우 유사하지만, 레이어 내부에 존재하는 개별 노드가 아닌 레이어 블록에서 작동한다는 점만 다릅니다. CCT에서, 확률적 깊이는 트랜스포머 인코더의 residual 블록 바로 직전에 사용됩니다.
# Referred from: github.com:rwightman/pytorch-image-models.
class StochasticDepth(layers.Layer):
def __init__(self, drop_prop, **kwargs):
super().__init__(**kwargs)
self.drop_prob = drop_prop
self.seed_generator = keras.random.SeedGenerator(1337)
def call(self, x, training=None):
if training:
keep_prob = 1 - self.drop_prob
shape = (keras.ops.shape(x)[0],) + (1,) * (len(x.shape) - 1)
random_tensor = keep_prob + keras.random.uniform(
shape, 0, 1, seed=self.seed_generator
)
random_tensor = keras.ops.floor(random_tensor)
return (x / keep_prob) * random_tensor
return x트랜스포머 인코더를 위한 MLP
def mlp(x, hidden_units, dropout_rate):
for units in hidden_units:
x = layers.Dense(units, activation=keras.ops.gelu)(x)
x = layers.Dropout(dropout_rate)(x)
return x데이터 보강
원본 논문에서, 저자는 AutoAugment을 사용하여 더 강력한 정규화를 유도합니다. 이 예제에서는, 랜덤 자르기(random cropping) 및 뒤집기와 같은 표준 기하학적 보강을 사용합니다.
# 리스케일링 레이어에 주목하세요. 이러한 레이어에는 사전 정의된 추론 동작이 있습니다.
data_augmentation = keras.Sequential(
[
layers.Rescaling(scale=1.0 / 255),
layers.RandomCrop(image_size, image_size),
layers.RandomFlip("horizontal"),
],
name="data_augmentation",
)최종 CCT 모델
CCT에서는, 트랜스포머 인코더의 출력에 가중치를 부여한 다음, 최종 작업별 레이어로 전달합니다. (이 예에서는 분류를 수행합니다)
def create_cct_model(
image_size=image_size,
input_shape=input_shape,
num_heads=num_heads,
projection_dim=projection_dim,
transformer_units=transformer_units,
):
inputs = layers.Input(input_shape)
# 데이터 보강.
augmented = data_augmentation(inputs)
# 패치 인코딩.
cct_tokenizer = CCTTokenizer()
encoded_patches = cct_tokenizer(augmented)
# 위치 임베딩 적용.
if positional_emb:
sequence_length = encoded_patches.shape[1]
encoded_patches += PositionEmbedding(sequence_length=sequence_length)(
encoded_patches
)
# 확률적 깊이 확률 계산하기.
dpr = [x for x in np.linspace(0, stochastic_depth_rate, transformer_layers)]
# 트랜스포머 블록의 여러 레이어 만들기.
for i in range(transformer_layers):
# 레이어 정규화 1.
x1 = layers.LayerNormalization(epsilon=1e-5)(encoded_patches)
# 멀티 헤드 어텐션 레이어 생성.
attention_output = layers.MultiHeadAttention(
num_heads=num_heads, key_dim=projection_dim, dropout=0.1
)(x1, x1)
# 스킵 연결 1.
attention_output = StochasticDepth(dpr[i])(attention_output)
x2 = layers.Add()([attention_output, encoded_patches])
# 레이어 정규화 2.
x3 = layers.LayerNormalization(epsilon=1e-5)(x2)
# MLP.
x3 = mlp(x3, hidden_units=transformer_units, dropout_rate=0.1)
# 스킵 연결 2.
x3 = StochasticDepth(dpr[i])(x3)
encoded_patches = layers.Add()([x3, x2])
# 시퀀스 풀링 적용.
representation = layers.LayerNormalization(epsilon=1e-5)(encoded_patches)
weighted_representation = SequencePooling()(representation)
# 출력 분류.
logits = layers.Dense(num_classes)(weighted_representation)
# Keras 모델 생성.
model = keras.Model(inputs=inputs, outputs=logits)
return model모델 트레이닝 및 평가
def run_experiment(model):
optimizer = keras.optimizers.AdamW(learning_rate=0.001, weight_decay=0.0001)
model.compile(
optimizer=optimizer,
loss=keras.losses.CategoricalCrossentropy(
from_logits=True, label_smoothing=0.1
),
metrics=[
keras.metrics.CategoricalAccuracy(name="accuracy"),
keras.metrics.TopKCategoricalAccuracy(5, name="top-5-accuracy"),
],
)
checkpoint_filepath = "/tmp/checkpoint.weights.h5"
checkpoint_callback = keras.callbacks.ModelCheckpoint(
checkpoint_filepath,
monitor="val_accuracy",
save_best_only=True,
save_weights_only=True,
)
history = model.fit(
x=x_train,
y=y_train,
batch_size=batch_size,
epochs=num_epochs,
validation_split=0.1,
callbacks=[checkpoint_callback],
)
model.load_weights(checkpoint_filepath)
_, accuracy, top_5_accuracy = model.evaluate(x_test, y_test)
print(f"Test accuracy: {round(accuracy * 100, 2)}%")
print(f"Test top 5 accuracy: {round(top_5_accuracy * 100, 2)}%")
return history
cct_model = create_cct_model()
history = run_experiment(cct_model)결과
Epoch 1/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 90s 248ms/step - accuracy: 0.2578 - loss: 2.0882 - top-5-accuracy: 0.7553 - val_accuracy: 0.4438 - val_loss: 1.6872 - val_top-5-accuracy: 0.9046
Epoch 2/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 91s 258ms/step - accuracy: 0.4779 - loss: 1.6074 - top-5-accuracy: 0.9261 - val_accuracy: 0.5730 - val_loss: 1.4462 - val_top-5-accuracy: 0.9562
Epoch 3/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 260ms/step - accuracy: 0.5655 - loss: 1.4371 - top-5-accuracy: 0.9501 - val_accuracy: 0.6178 - val_loss: 1.3458 - val_top-5-accuracy: 0.9626
Epoch 4/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 261ms/step - accuracy: 0.6166 - loss: 1.3343 - top-5-accuracy: 0.9613 - val_accuracy: 0.6610 - val_loss: 1.2695 - val_top-5-accuracy: 0.9706
Epoch 5/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 261ms/step - accuracy: 0.6468 - loss: 1.2814 - top-5-accuracy: 0.9672 - val_accuracy: 0.6834 - val_loss: 1.2231 - val_top-5-accuracy: 0.9716
Epoch 6/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 261ms/step - accuracy: 0.6619 - loss: 1.2412 - top-5-accuracy: 0.9708 - val_accuracy: 0.6842 - val_loss: 1.2018 - val_top-5-accuracy: 0.9744
Epoch 7/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 263ms/step - accuracy: 0.6976 - loss: 1.1775 - top-5-accuracy: 0.9752 - val_accuracy: 0.6988 - val_loss: 1.1988 - val_top-5-accuracy: 0.9752
Epoch 8/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 263ms/step - accuracy: 0.7070 - loss: 1.1579 - top-5-accuracy: 0.9774 - val_accuracy: 0.7010 - val_loss: 1.1780 - val_top-5-accuracy: 0.9732
Epoch 9/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 95s 269ms/step - accuracy: 0.7219 - loss: 1.1255 - top-5-accuracy: 0.9795 - val_accuracy: 0.7166 - val_loss: 1.1375 - val_top-5-accuracy: 0.9784
Epoch 10/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 264ms/step - accuracy: 0.7273 - loss: 1.1087 - top-5-accuracy: 0.9801 - val_accuracy: 0.7258 - val_loss: 1.1286 - val_top-5-accuracy: 0.9814
Epoch 11/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 265ms/step - accuracy: 0.7361 - loss: 1.0863 - top-5-accuracy: 0.9828 - val_accuracy: 0.7222 - val_loss: 1.1412 - val_top-5-accuracy: 0.9766
Epoch 12/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 264ms/step - accuracy: 0.7504 - loss: 1.0644 - top-5-accuracy: 0.9834 - val_accuracy: 0.7418 - val_loss: 1.0943 - val_top-5-accuracy: 0.9812
Epoch 13/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 94s 266ms/step - accuracy: 0.7593 - loss: 1.0422 - top-5-accuracy: 0.9856 - val_accuracy: 0.7468 - val_loss: 1.0834 - val_top-5-accuracy: 0.9818
Epoch 14/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 265ms/step - accuracy: 0.7647 - loss: 1.0307 - top-5-accuracy: 0.9868 - val_accuracy: 0.7526 - val_loss: 1.0863 - val_top-5-accuracy: 0.9822
Epoch 15/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 263ms/step - accuracy: 0.7684 - loss: 1.0231 - top-5-accuracy: 0.9863 - val_accuracy: 0.7666 - val_loss: 1.0454 - val_top-5-accuracy: 0.9834
Epoch 16/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 94s 268ms/step - accuracy: 0.7809 - loss: 1.0007 - top-5-accuracy: 0.9859 - val_accuracy: 0.7670 - val_loss: 1.0469 - val_top-5-accuracy: 0.9838
Epoch 17/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 94s 268ms/step - accuracy: 0.7902 - loss: 0.9795 - top-5-accuracy: 0.9895 - val_accuracy: 0.7676 - val_loss: 1.0396 - val_top-5-accuracy: 0.9836
Epoch 18/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 106s 301ms/step - accuracy: 0.7920 - loss: 0.9693 - top-5-accuracy: 0.9889 - val_accuracy: 0.7616 - val_loss: 1.0791 - val_top-5-accuracy: 0.9828
Epoch 19/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 264ms/step - accuracy: 0.7965 - loss: 0.9631 - top-5-accuracy: 0.9893 - val_accuracy: 0.7850 - val_loss: 1.0149 - val_top-5-accuracy: 0.9842
Epoch 20/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 93s 265ms/step - accuracy: 0.8030 - loss: 0.9529 - top-5-accuracy: 0.9899 - val_accuracy: 0.7898 - val_loss: 1.0029 - val_top-5-accuracy: 0.9852
Epoch 21/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 261ms/step - accuracy: 0.8118 - loss: 0.9322 - top-5-accuracy: 0.9903 - val_accuracy: 0.7728 - val_loss: 1.0529 - val_top-5-accuracy: 0.9850
Epoch 22/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 91s 259ms/step - accuracy: 0.8104 - loss: 0.9308 - top-5-accuracy: 0.9906 - val_accuracy: 0.7874 - val_loss: 1.0090 - val_top-5-accuracy: 0.9876
Epoch 23/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 263ms/step - accuracy: 0.8164 - loss: 0.9193 - top-5-accuracy: 0.9911 - val_accuracy: 0.7800 - val_loss: 1.0091 - val_top-5-accuracy: 0.9844
Epoch 24/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 94s 268ms/step - accuracy: 0.8147 - loss: 0.9184 - top-5-accuracy: 0.9919 - val_accuracy: 0.7854 - val_loss: 1.0260 - val_top-5-accuracy: 0.9856
Epoch 25/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 262ms/step - accuracy: 0.8255 - loss: 0.9000 - top-5-accuracy: 0.9914 - val_accuracy: 0.7918 - val_loss: 1.0014 - val_top-5-accuracy: 0.9842
Epoch 26/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 90s 257ms/step - accuracy: 0.8297 - loss: 0.8865 - top-5-accuracy: 0.9933 - val_accuracy: 0.7924 - val_loss: 1.0065 - val_top-5-accuracy: 0.9834
Epoch 27/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 262ms/step - accuracy: 0.8339 - loss: 0.8837 - top-5-accuracy: 0.9931 - val_accuracy: 0.7906 - val_loss: 1.0035 - val_top-5-accuracy: 0.9870
Epoch 28/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 260ms/step - accuracy: 0.8362 - loss: 0.8781 - top-5-accuracy: 0.9934 - val_accuracy: 0.7878 - val_loss: 1.0041 - val_top-5-accuracy: 0.9850
Epoch 29/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 260ms/step - accuracy: 0.8398 - loss: 0.8707 - top-5-accuracy: 0.9942 - val_accuracy: 0.7854 - val_loss: 1.0186 - val_top-5-accuracy: 0.9858
Epoch 30/30
352/352 ━━━━━━━━━━━━━━━━━━━━ 92s 263ms/step - accuracy: 0.8438 - loss: 0.8614 - top-5-accuracy: 0.9933 - val_accuracy: 0.7892 - val_loss: 1.0123 - val_top-5-accuracy: 0.9846
313/313 ━━━━━━━━━━━━━━━━━━━━ 14s 44ms/step - accuracy: 0.7752 - loss: 1.0370 - top-5-accuracy: 0.9824
Test accuracy: 77.82%
Test top 5 accuracy: 98.42%Let’s now visualize the training progress of the model.
plt.plot(history.history["loss"], label="train_loss")
plt.plot(history.history["val_loss"], label="val_loss")
plt.xlabel("Epochs")
plt.ylabel("Loss")
plt.title("Train and Validation Losses Over Epochs", fontsize=14)
plt.legend()
plt.grid()
plt.show()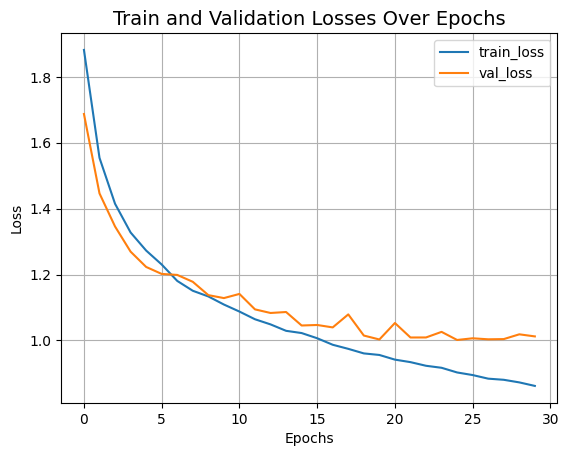
방금 트레이닝한 CCT 모델은 0.4백만개의 파라미터로, 30 에포크 안에 ~79%의 top-1 정확도에 도달했습니다. 위의 그래프에서도 과적합의 징후는 보이지 않습니다. 즉, 이 네트워크를 더 오래 트레이닝할 수 있으며(아마도 정규화를 통해 조금 더) 더 나은 성능을 얻을 수 있습니다. 이 성능은 코사인 감쇠 학습률 스케줄, AutoAugment, MixUp, Cutmix와 같은 다른 데이터 보강 기법과 같은 추가 레시피로 더욱 향상될 수 있습니다. 이러한 수정을 통해, 저자는 CIFAR-10 데이터 세트에 대해 95.1%의 top-1 정확도를 달성했음을 보여줍니다. 또한 저자는 컨볼루션 블록 수, 트랜스포머 레이어 등이 CCT의 최종 성능에 어떤 영향을 미치는지 연구하기 위해 여러 실험을 제시합니다.
비교를 위해, ViT 모델이 CIFAR-10 데이터 세트에 대해 78.22%의 top-1 정확도에 도달하려면 약 470만개의 파라미터와 100 에포크의 트레이닝이 필요합니다. 실험 설정에 대한 자세한 내용은 이 노트북을 참조하세요.
또한 저자들은 NLP 작업에서 콤팩트 컨볼루션 트랜스포머의 성능을 시연하고 경쟁력 있는 결과를 보고합니다.