Vector-Quantized Variational Autoencoders
- 원본 링크 : https://keras.io/examples/generative/vq_vae/
- 최종 확인 : 2024-11-23
저자 : Sayak Paul
생성일 : 2021/07/21
최종 편집일 : 2021/06/27
설명 : 이미지 재구성과 생성에 대한 코드북 샘플링을 위한 VQ-VAE 트레이닝
이 예제에서는, 벡터 양자화 변이형 오토인코더(VQ-VAE, Vector Quantized Variational Autoencoder)를 개발합니다. VQ-VAE는 van der Oord 등이 Neural Discrete Representation Learning에서 제안하였습니다. 표준 VAE에서는 잠재 공간이 연속적이며, 가우시안 분포에서 샘플링됩니다. 이러한 연속적인 분포를 그래디언트 디센트를 통해 학습하는 것은 일반적으로 어렵습니다. 반면, VQ-VAE는 이산적인 잠재 공간에서 동작하여, 최적화 문제를 더 단순하게 만듭니다. 이는 코드북 을 유지하여 이뤄집니다. 코드북은 연속적인 임베딩과 인코딩된 출력 간의 거리를 이산화함으로써 개발됩니다. 이 이산적인 코드 단어들은 디코더로 전달되어, 재구성된 샘플을 생성하도록 트레이닝됩니다.
VQ-VAE에 대한 개요는, 원 논문 및 이 비디오 설명을 참고하십시오. VAE에 대한 복습이 필요하다면, 이 책의 챕터를 참조할 수 있습니다. VQ-VAE는 DALL-E의 주요 구성 요소 중 하나이며, 코드북 아이디어는 VQ-GANs에서도 사용됩니다.
이 예제는 DeepMind의 공식 VQ-VAE 튜토리얼에서 구현 세부 사항을 가져옵니다.
요구사항
이 예제를 실행하려면, TensorFlow 2.5 이상과 TensorFlow Probability가 필요합니다. 아래 명령어로 설치할 수 있습니다.
!pip install -q tensorflow-probabilityImports
import numpy as np
import matplotlib.pyplot as plt
from tensorflow import keras
from tensorflow.keras import layers
import tensorflow_probability as tfp
import tensorflow as tfVectorQuantizer 레이어
먼저, 인코더와 디코더 사이에 위치한, 벡터 양자화를 위한, 커스텀 레이어를 구현합니다.
인코더 출력의 모양이 (batch_size, height, width, num_filters)일 때,
벡터 양자화는 먼저 이 출력을 평탄화(flatten)하여, num_filters 차원만 유지합니다.
따라서 모양은 (batch_size * height * width, num_filters)로 변환됩니다.
이 과정을 통해 전체 필터 수를 잠재 임베딩의 크기로 취급하게 됩니다.
그 후 코드북을 학습할 수 있도록 임베딩 테이블을 초기화합니다. 평탄화된 인코더 출력과 코드북의 코드 단어 간의 L2-정규화 거리를 측정한 후, 최소 거리를 제공하는 코드를 선택하여, 원-핫 인코딩을 적용해 양자화를 수행합니다. 이 방법을 통해 해당 인코더 출력과 최소 거리를 가진 코드는 1로, 나머지 코드는 0으로 매핑됩니다.
양자화 과정은 미분 불가능하므로, 스트레이트-스루 추정기(straight-through estimator)를 디코더와 인코더 사이에 적용하여, 디코더의 그래디언트가 직접 인코더로 전파되도록 합니다. 인코더와 디코더가 동일한 채널 공간을 공유하므로, 디코더의 그래디언트는 여전히 인코더에 의미가 있습니다.
class VectorQuantizer(layers.Layer):
def __init__(self, num_embeddings, embedding_dim, beta=0.25, **kwargs):
super().__init__(**kwargs)
self.embedding_dim = embedding_dim
self.num_embeddings = num_embeddings
# 논문에 따르면, `beta` 값은 [0.25, 2] 사이로 유지하는 것이 좋습니다.
self.beta = beta
# 양자화할 임베딩을 초기화합니다.
w_init = tf.random_uniform_initializer()
self.embeddings = tf.Variable(
initial_value=w_init(
shape=(self.embedding_dim, self.num_embeddings), dtype="float32"
),
trainable=True,
name="embeddings_vqvae",
)
def call(self, x):
# 입력의 모양을 계산하고,
# `embedding_dim`을 유지하면서 입력을 평탄화합니다.
input_shape = tf.shape(x)
flattened = tf.reshape(x, [-1, self.embedding_dim])
# 양자화하기.
encoding_indices = self.get_code_indices(flattened)
encodings = tf.one_hot(encoding_indices, self.num_embeddings)
quantized = tf.matmul(encodings, self.embeddings, transpose_b=True)
# 양자화된 값을 원래의 입력 모양으로 다시 reshape 합니다.
quantized = tf.reshape(quantized, input_shape)
# 벡터 양자화 손실을 계산하여 레이어에 추가합니다.
# 손실을 레이어에 추가하는 방법은 여기서 확인할 수 있습니다:
# https://keras.io/guides/making_new_layers_and_models_via_subclassing/
# 원 논문에서 손실 함수의 수식을 참고하십시오.
commitment_loss = tf.reduce_mean((tf.stop_gradient(quantized) - x) ** 2)
codebook_loss = tf.reduce_mean((quantized - tf.stop_gradient(x)) ** 2)
self.add_loss(self.beta * commitment_loss + codebook_loss)
# 스트레이트-스루 추정기.
quantized = x + tf.stop_gradient(quantized - x)
return quantized
def get_code_indices(self, flattened_inputs):
# 입력과 코드 간의 L2-정규화 거리를 계산합니다.
similarity = tf.matmul(flattened_inputs, self.embeddings)
distances = (
tf.reduce_sum(flattened_inputs ** 2, axis=1, keepdims=True)
+ tf.reduce_sum(self.embeddings ** 2, axis=0)
- 2 * similarity
)
# 최소 거리에 해당하는 인덱스를 도출합니다.
encoding_indices = tf.argmin(distances, axis=1)
return encoding_indices스트레이트-스루 추정에 대한 설명:
이 코드 라인은 스트레이트-스루 추정 부분을 수행합니다: quantized = x + tf.stop_gradient(quantized - x).
역전파 시, (quantized - x)는 계산 그래프에 포함되지 않으며,
quantized에 대해 계산된 그래디언트가 inputs에 복사됩니다.
이 기술에 대한 이해를 도와준 이 비디오에 감사드립니다.
인코더 및 디코더
이제 VQ-VAE의 인코더와 디코더를 구현하겠습니다. 우리는 MNIST 데이터셋에 적합한 용량을 갖도록 인코더와 디코더를 작게 유지할 것입니다. 인코더와 디코더의 구현은 이 예제에서 가져왔습니다.
참고로, 양자화 아키텍처의 인코더 및 디코더 레이어에서는 ReLU 이외의 활성화 함수 는 잘 작동하지 않을 수 있습니다. 예를 들어, Leaky ReLU 활성화 레이어는, 트레이닝이 어려워져 간헐적인 손실 급증이 발생할 수 있으며, 모델이 이를 회복하는 데 어려움을 겪는 경우가 있습니다.
def get_encoder(latent_dim=16):
encoder_inputs = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(32, 3, activation="relu", strides=2, padding="same")(
encoder_inputs
)
x = layers.Conv2D(64, 3, activation="relu", strides=2, padding="same")(x)
encoder_outputs = layers.Conv2D(latent_dim, 1, padding="same")(x)
return keras.Model(encoder_inputs, encoder_outputs, name="encoder")
def get_decoder(latent_dim=16):
latent_inputs = keras.Input(shape=get_encoder(latent_dim).output.shape[1:])
x = layers.Conv2DTranspose(64, 3, activation="relu", strides=2, padding="same")(
latent_inputs
)
x = layers.Conv2DTranspose(32, 3, activation="relu", strides=2, padding="same")(x)
decoder_outputs = layers.Conv2DTranspose(1, 3, padding="same")(x)
return keras.Model(latent_inputs, decoder_outputs, name="decoder")독립형 VQ-VAE 모델
def get_vqvae(latent_dim=16, num_embeddings=64):
vq_layer = VectorQuantizer(num_embeddings, latent_dim, name="vector_quantizer")
encoder = get_encoder(latent_dim)
decoder = get_decoder(latent_dim)
inputs = keras.Input(shape=(28, 28, 1))
encoder_outputs = encoder(inputs)
quantized_latents = vq_layer(encoder_outputs)
reconstructions = decoder(quantized_latents)
return keras.Model(inputs, reconstructions, name="vq_vae")
get_vqvae().summary()결과
Model: "vq_vae"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_4 (InputLayer) [(None, 28, 28, 1)] 0
_________________________________________________________________
encoder (Functional) (None, 7, 7, 16) 19856
_________________________________________________________________
vector_quantizer (VectorQuan (None, 7, 7, 16) 1024
_________________________________________________________________
decoder (Functional) (None, 28, 28, 1) 28033
=================================================================
Total params: 48,913
Trainable params: 48,913
Non-trainable params: 0
_________________________________________________________________참고: 인코더의 출력 채널 수는 벡터 양자화기(quantizer)를 위한 latent_dim과 일치해야 합니다.
VQVAETrainer 내에서 트레이닝 루프 래핑
class VQVAETrainer(keras.models.Model):
def __init__(self, train_variance, latent_dim=32, num_embeddings=128, **kwargs):
super().__init__(**kwargs)
self.train_variance = train_variance
self.latent_dim = latent_dim
self.num_embeddings = num_embeddings
# VQ-VAE 모델 생성
self.vqvae = get_vqvae(self.latent_dim, self.num_embeddings)
# 손실 추적을 위한 메트릭 정의
self.total_loss_tracker = keras.metrics.Mean(name="total_loss")
self.reconstruction_loss_tracker = keras.metrics.Mean(
name="reconstruction_loss"
)
self.vq_loss_tracker = keras.metrics.Mean(name="vq_loss")
@property
def metrics(self):
# 메트릭 반환
return [
self.total_loss_tracker,
self.reconstruction_loss_tracker,
self.vq_loss_tracker,
]
def train_step(self, x):
# GradientTape를 사용한 자동 미분
with tf.GradientTape() as tape:
# VQ-VAE로부터의 출력
reconstructions = self.vqvae(x)
# 손실 계산 (복원 손실 + VQ-VAE의 손실)
reconstruction_loss = (
tf.reduce_mean((x - reconstructions) ** 2) / self.train_variance
)
total_loss = reconstruction_loss + sum(self.vqvae.losses)
# 역전파를 통한 가중치 업데이트
grads = tape.gradient(total_loss, self.vqvae.trainable_variables)
self.optimizer.apply_gradients(zip(grads, self.vqvae.trainable_variables))
# 손실 추적
self.total_loss_tracker.update_state(total_loss)
self.reconstruction_loss_tracker.update_state(reconstruction_loss)
self.vq_loss_tracker.update_state(sum(self.vqvae.losses))
# 결과 로그 반환
return {
"loss": self.total_loss_tracker.result(),
"reconstruction_loss": self.reconstruction_loss_tracker.result(),
"vqvae_loss": self.vq_loss_tracker.result(),
}MNIST 데이터셋 로드 및 전처리
(x_train, _), (x_test, _) = keras.datasets.mnist.load_data()
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)
x_train_scaled = (x_train / 255.0) - 0.5
x_test_scaled = (x_test / 255.0) - 0.5
data_variance = np.var(x_train / 255.0)결과
Downloading data from https://storage.googleapis.com/tensorflow/tf-keras-datasets/mnist.npz
11493376/11490434 [==============================] - 0s 0us/stepVQ-VAE 모델 트레이닝
vqvae_trainer = VQVAETrainer(data_variance, latent_dim=16, num_embeddings=128)
vqvae_trainer.compile(optimizer=keras.optimizers.Adam())
vqvae_trainer.fit(x_train_scaled, epochs=30, batch_size=128)결과
Epoch 1/30
469/469 [==============================] - 18s 6ms/step - loss: 2.2962 - reconstruction_loss: 0.3869 - vqvae_loss: 1.5950
Epoch 2/30
469/469 [==============================] - 3s 6ms/step - loss: 2.2980 - reconstruction_loss: 0.1692 - vqvae_loss: 2.1108
Epoch 3/30
469/469 [==============================] - 3s 6ms/step - loss: 1.1356 - reconstruction_loss: 0.1281 - vqvae_loss: 0.9997
Epoch 4/30
469/469 [==============================] - 3s 6ms/step - loss: 0.6112 - reconstruction_loss: 0.1030 - vqvae_loss: 0.5031
Epoch 5/30
469/469 [==============================] - 3s 6ms/step - loss: 0.4375 - reconstruction_loss: 0.0883 - vqvae_loss: 0.3464
Epoch 6/30
469/469 [==============================] - 3s 6ms/step - loss: 0.3579 - reconstruction_loss: 0.0788 - vqvae_loss: 0.2775
Epoch 7/30
469/469 [==============================] - 3s 5ms/step - loss: 0.3197 - reconstruction_loss: 0.0725 - vqvae_loss: 0.2457
Epoch 8/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2960 - reconstruction_loss: 0.0673 - vqvae_loss: 0.2277
Epoch 9/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2798 - reconstruction_loss: 0.0640 - vqvae_loss: 0.2152
Epoch 10/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2681 - reconstruction_loss: 0.0612 - vqvae_loss: 0.2061
Epoch 11/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2578 - reconstruction_loss: 0.0590 - vqvae_loss: 0.1986
Epoch 12/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2551 - reconstruction_loss: 0.0574 - vqvae_loss: 0.1974
Epoch 13/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2526 - reconstruction_loss: 0.0560 - vqvae_loss: 0.1961
Epoch 14/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2485 - reconstruction_loss: 0.0546 - vqvae_loss: 0.1936
Epoch 15/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2462 - reconstruction_loss: 0.0533 - vqvae_loss: 0.1926
Epoch 16/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2445 - reconstruction_loss: 0.0523 - vqvae_loss: 0.1920
Epoch 17/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2427 - reconstruction_loss: 0.0515 - vqvae_loss: 0.1911
Epoch 18/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2405 - reconstruction_loss: 0.0505 - vqvae_loss: 0.1898
Epoch 19/30
469/469 [==============================] - 3s 6ms/step - loss: 0.2368 - reconstruction_loss: 0.0495 - vqvae_loss: 0.1871
Epoch 20/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2310 - reconstruction_loss: 0.0486 - vqvae_loss: 0.1822
Epoch 21/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2245 - reconstruction_loss: 0.0475 - vqvae_loss: 0.1769
Epoch 22/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2205 - reconstruction_loss: 0.0469 - vqvae_loss: 0.1736
Epoch 23/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2195 - reconstruction_loss: 0.0465 - vqvae_loss: 0.1730
Epoch 24/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2187 - reconstruction_loss: 0.0461 - vqvae_loss: 0.1726
Epoch 25/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2180 - reconstruction_loss: 0.0458 - vqvae_loss: 0.1721
Epoch 26/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2163 - reconstruction_loss: 0.0454 - vqvae_loss: 0.1709
Epoch 27/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2156 - reconstruction_loss: 0.0452 - vqvae_loss: 0.1704
Epoch 28/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2146 - reconstruction_loss: 0.0449 - vqvae_loss: 0.1696
Epoch 29/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2139 - reconstruction_loss: 0.0447 - vqvae_loss: 0.1692
Epoch 30/30
469/469 [==============================] - 3s 5ms/step - loss: 0.2127 - reconstruction_loss: 0.0444 - vqvae_loss: 0.1682
<tensorflow.python.keras.callbacks.History at 0x7f96402f4e50>테스트 세트에 대한 복원 결과
def show_subplot(original, reconstructed):
plt.subplot(1, 2, 1)
plt.imshow(original.squeeze() + 0.5)
plt.title("Original")
plt.axis("off")
plt.subplot(1, 2, 2)
plt.imshow(reconstructed.squeeze() + 0.5)
plt.title("Reconstructed")
plt.axis("off")
plt.show()
trained_vqvae_model = vqvae_trainer.vqvae
idx = np.random.choice(len(x_test_scaled), 10)
test_images = x_test_scaled[idx]
reconstructions_test = trained_vqvae_model.predict(test_images)
for test_image, reconstructed_image in zip(test_images, reconstructions_test):
show_subplot(test_image, reconstructed_image)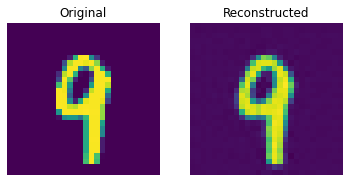
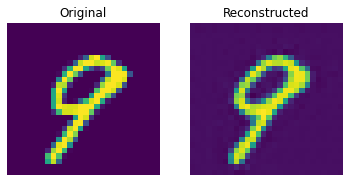

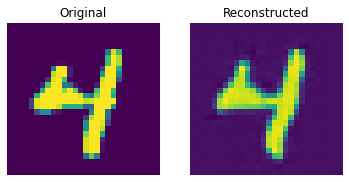
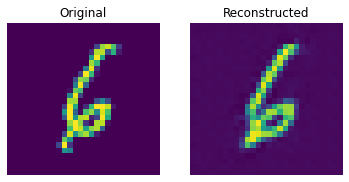
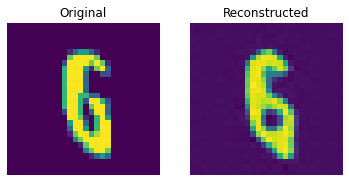
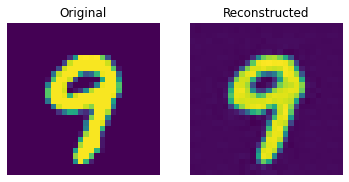
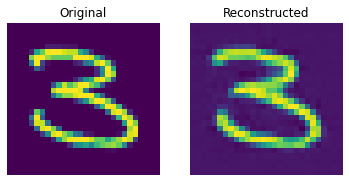
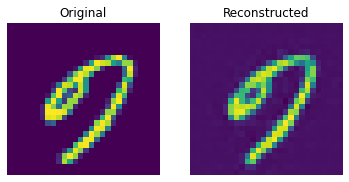
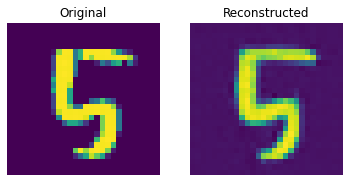
이 결과는 꽤 괜찮습니다. 다양한 하이퍼파라미터(특히 임베딩의 개수와 임베딩의 차원)를 변경하면서, 결과에 어떤 영향을 미치는지 확인해보세요.
이산 코드 시각화
encoder = vqvae_trainer.vqvae.get_layer("encoder")
quantizer = vqvae_trainer.vqvae.get_layer("vector_quantizer")
encoded_outputs = encoder.predict(test_images)
flat_enc_outputs = encoded_outputs.reshape(-1, encoded_outputs.shape[-1])
codebook_indices = quantizer.get_code_indices(flat_enc_outputs)
codebook_indices = codebook_indices.numpy().reshape(encoded_outputs.shape[:-1])
for i in range(len(test_images)):
plt.subplot(1, 2, 1)
plt.imshow(test_images[i].squeeze() + 0.5)
plt.title("Original")
plt.axis("off")
plt.subplot(1, 2, 2)
plt.imshow(codebook_indices[i])
plt.title("Code")
plt.axis("off")
plt.show()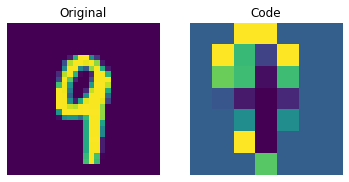


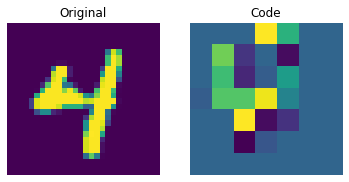
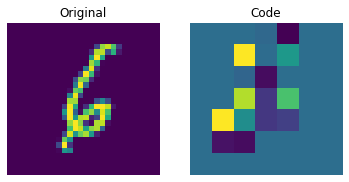
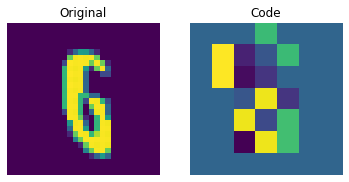
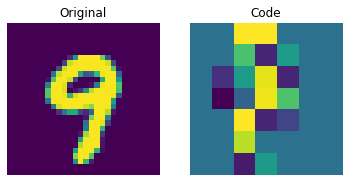


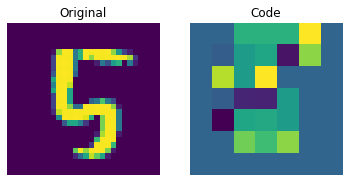
위의 그림은 이산 코드가 데이터셋에서 일부 규칙성을 포착할 수 있음을 보여줍니다. 이제, 이 코드북을 사용하여 새로운 이미지를 생성하려면 어떻게 해야 할까요? 이 코드는 이산적이며 카테고리 분포를 따르므로, 우리가 해석 가능한 코드 시퀀스를 생성할 수 있을 때까지 의미 있는 것을 생성하는 데 사용할 수 없습니다. 저자는 이러한 코드를 트레이닝하여, 새로운 예제를 생성할 수 있는 강력한 사전 확률(priors)로 사용할 수 있도록 PixelCNN을 사용합니다. PixelCNN은 van der Oord 등이 제안한 Conditional Image Generation with PixelCNN Decoders 논문에 처음 등장했습니다. 우리는 이 예제에서 PixelCNN 구현을 차용할 것입니다. PixelCNN은 자기 회귀(autoregressive) 생성 모델로, 출력은 이전에 생성된(prior ones) 것에 대해 conditional 입니다. 다시 말해, PixelCNN은 이미지를 픽셀 단위로 생성합니다. 하지만, 이 예제에서는 PixelCNN이 픽셀을 직접 생성하는 대신, 코드북 인덱스를 생성하는 작업을 수행합니다. 트레이닝된 VQ-VAE 디코더는 PixelCNN이 생성한 인덱스를 다시 픽셀 공간으로 매핑하는 데 사용됩니다.
PixelCNN 하이퍼파라미터
num_residual_blocks = 2
num_pixelcnn_layers = 2
pixelcnn_input_shape = encoded_outputs.shape[1:-1]
print(f"Input shape of the PixelCNN: {pixelcnn_input_shape}")결과
Input shape of the PixelCNN: (7, 7)이 입력 형태는 인코더에 의해 수행된 해상도 감소를 나타냅니다. “same” 패딩을 사용하면, 각 stride-2 컨볼루션 레이어에 대해 출력 모양의 해상도가 정확히 절반으로 줄어듭니다. 따라서, 이 두 레이어를 사용하면, 인코더 출력 텐서가 축 2와 3에 대해 7x7로 끝나며, 첫 번째 축은 배치 크기이고, 마지막 축은 코드북 임베딩 크기입니다. 오토인코더의 양자화(quantization) 레이어는 이 7x7 텐서를 코드북의 인덱스로 매핑하므로, PixelCNN은 입력 모양으로 이 출력 레이어 축 크기를 일치시켜야 합니다. 이 아키텍처에서 PixelCNN의 작업은 코드북 인덱스의 가능한(likely) 7x7 배열을 생성하는 것입니다.
이 모양는 더 큰 크기의 이미지 도메인에서 최적화해야 할 요소입니다. PixelCNN은 자기 회귀적(autoregressive)이므로, 코드북 인덱스를 순차적으로 처리해야 새로운 이미지를 생성할 수 있습니다. 각 stride-2 (정확히는 스트라이드 (2, 2)) 컨볼루션 레이어는 이미지 생성 시간을 4배로 나누어줍니다. 그러나, 이미지 복원에 필요한 코드 수가 너무 적으면, 디코더가 이미지의 세부 정보를 표현하기에 충분한 정보가 없어 출력 품질이 저하될 수 있습니다. 이를 어느 정도 개선할 수 있는 방법은 더 큰 코드북을 사용하는 것입니다. 이미지 생성 절차의 자기 회귀 부분은 코드북 인덱스를 사용하므로, 더 큰 코드북을 사용하는 성능 저하는 거의 없습니다. 코드북 크기가 크더라도 코드북에서 코드를 조회하는 시간은 코드북 인덱스 시퀀스를 반복하는 시간에 비해 훨씬 짧기 때문에, 코드북 크기는 배치 크기에만 영향을 미칩니다. 이러한 절충점을 최적화하려면 아키텍처를 조정해야 할 수 있으며, 데이터셋에 따라 다를 수 있습니다.
PixelCNN 모델
대부분은 이 예제에서 가져온 것입니다.
참고 사항
이 예제의 수정 및 코드 정리에 도움을 주신, Rein van ’t Veer님께 감사드립니다.
# 첫 번째 레이어는 PixelCNN 레이어입니다.
# 이 레이어는 2D 컨볼루션 레이어에 마스킹을 추가하여 작동합니다.
class PixelConvLayer(layers.Layer):
def __init__(self, mask_type, **kwargs):
super().__init__()
self.mask_type = mask_type
self.conv = layers.Conv2D(**kwargs)
def build(self, input_shape):
# Conv2D 레이어를 빌드하여 커널 변수를 초기화합니다.
self.conv.build(input_shape)
# 초기화된 커널을 사용하여 마스크를 생성합니다.
kernel_shape = self.conv.kernel.get_shape()
self.mask = np.zeros(shape=kernel_shape)
self.mask[: kernel_shape[0] // 2, ...] = 1.0
self.mask[kernel_shape[0] // 2, : kernel_shape[1] // 2, ...] = 1.0
if self.mask_type == "B":
self.mask[kernel_shape[0] // 2, kernel_shape[1] // 2, ...] = 1.0
def call(self, inputs):
self.conv.kernel.assign(self.conv.kernel * self.mask)
return self.conv(inputs)
# 다음으로, Residual Block 레이어를 빌드합니다.
# 이 레이어는 PixelConvLayer를 기반으로 한, 일반적인 Residual Block입니다.
class ResidualBlock(keras.layers.Layer):
def __init__(self, filters, **kwargs):
super().__init__(**kwargs)
self.conv1 = keras.layers.Conv2D(
filters=filters, kernel_size=1, activation="relu"
)
self.pixel_conv = PixelConvLayer(
mask_type="B",
filters=filters // 2,
kernel_size=3,
activation="relu",
padding="same",
)
self.conv2 = keras.layers.Conv2D(
filters=filters, kernel_size=1, activation="relu"
)
def call(self, inputs):
x = self.conv1(inputs)
x = self.pixel_conv(x)
x = self.conv2(x)
return keras.layers.add([inputs, x])
# PixelCNN 모델 빌드
pixelcnn_inputs = keras.Input(shape=pixelcnn_input_shape, dtype=tf.int32)
ohe = tf.one_hot(pixelcnn_inputs, vqvae_trainer.num_embeddings)
x = PixelConvLayer(
mask_type="A", filters=128, kernel_size=7, activation="relu", padding="same"
)(ohe)
for _ in range(num_residual_blocks):
x = ResidualBlock(filters=128)(x)
for _ in range(num_pixelcnn_layers):
x = PixelConvLayer(
mask_type="B",
filters=128,
kernel_size=1,
strides=1,
activation="relu",
padding="valid",
)(x)
out = keras.layers.Conv2D(
filters=vqvae_trainer.num_embeddings, kernel_size=1, strides=1, padding="valid"
)(x)
pixel_cnn = keras.Model(pixelcnn_inputs, out, name="pixel_cnn")
pixel_cnn.summary()결과
Model: "pixel_cnn"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
input_9 (InputLayer) [(None, 7, 7)] 0
_________________________________________________________________
tf.one_hot (TFOpLambda) (None, 7, 7, 128) 0
_________________________________________________________________
pixel_conv_layer (PixelConvL (None, 7, 7, 128) 802944
_________________________________________________________________
residual_block (ResidualBloc (None, 7, 7, 128) 98624
_________________________________________________________________
residual_block_1 (ResidualBl (None, 7, 7, 128) 98624
_________________________________________________________________
pixel_conv_layer_3 (PixelCon (None, 7, 7, 128) 16512
_________________________________________________________________
pixel_conv_layer_4 (PixelCon (None, 7, 7, 128) 16512
_________________________________________________________________
conv2d_21 (Conv2D) (None, 7, 7, 128) 16512
=================================================================
Total params: 1,049,728
Trainable params: 1,049,728
Non-trainable params: 0
_________________________________________________________________PixelCNN을 트레이닝하기 위한 데이터 준비
PixelCNN을 트레이닝하여 이산 코드의 카테고리 분포를 학습할 것입니다. 먼저, 우리가 트레이닝한 인코더와 벡터 양자화기(quantizer)를 사용하여 코드 인덱스를 생성합니다. 우리의 트레이닝 목표는 이러한 인덱스와 PixelCNN 출력 간의 교차 엔트로피 손실을 최소화하는 것입니다. 여기서, 카테고리의 수는 코드북에 존재하는 임베딩의 수(우리의 경우 128)와 같습니다. PixelCNN 모델은 분포를 학습하도록 트레이닝되며(L1/L2 손실을 최소화하는 것이 아닌), 이는 PixelCNN이 생성 능력을 얻는 이유입니다.
# 코드북 인덱스를 생성합니다.
encoded_outputs = encoder.predict(x_train_scaled)
flat_enc_outputs = encoded_outputs.reshape(-1, encoded_outputs.shape[-1])
codebook_indices = quantizer.get_code_indices(flat_enc_outputs)
codebook_indices = codebook_indices.numpy().reshape(encoded_outputs.shape[:-1])
print(f"Shape of the training data for PixelCNN: {codebook_indices.shape}")결과
Shape of the training data for PixelCNN: (60000, 7, 7)PixelCNN 트레이닝
pixel_cnn.compile(
optimizer=keras.optimizers.Adam(3e-4),
loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
metrics=["accuracy"],
)
pixel_cnn.fit(
x=codebook_indices,
y=codebook_indices,
batch_size=128,
epochs=30,
validation_split=0.1,
)결과
Epoch 1/30
422/422 [==============================] - 4s 8ms/step - loss: 1.8550 - accuracy: 0.5959 - val_loss: 1.3127 - val_accuracy: 0.6268
Epoch 2/30
422/422 [==============================] - 3s 7ms/step - loss: 1.2207 - accuracy: 0.6402 - val_loss: 1.1722 - val_accuracy: 0.6482
Epoch 3/30
422/422 [==============================] - 3s 7ms/step - loss: 1.1412 - accuracy: 0.6536 - val_loss: 1.1313 - val_accuracy: 0.6552
Epoch 4/30
422/422 [==============================] - 3s 7ms/step - loss: 1.1060 - accuracy: 0.6601 - val_loss: 1.1058 - val_accuracy: 0.6596
Epoch 5/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0828 - accuracy: 0.6646 - val_loss: 1.1020 - val_accuracy: 0.6603
Epoch 6/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0649 - accuracy: 0.6682 - val_loss: 1.0809 - val_accuracy: 0.6638
Epoch 7/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0515 - accuracy: 0.6710 - val_loss: 1.0712 - val_accuracy: 0.6659
Epoch 8/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0406 - accuracy: 0.6733 - val_loss: 1.0647 - val_accuracy: 0.6671
Epoch 9/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0312 - accuracy: 0.6752 - val_loss: 1.0633 - val_accuracy: 0.6674
Epoch 10/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0235 - accuracy: 0.6771 - val_loss: 1.0554 - val_accuracy: 0.6695
Epoch 11/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0162 - accuracy: 0.6788 - val_loss: 1.0518 - val_accuracy: 0.6694
Epoch 12/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0105 - accuracy: 0.6799 - val_loss: 1.0541 - val_accuracy: 0.6693
Epoch 13/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0050 - accuracy: 0.6811 - val_loss: 1.0481 - val_accuracy: 0.6705
Epoch 14/30
422/422 [==============================] - 3s 7ms/step - loss: 1.0011 - accuracy: 0.6820 - val_loss: 1.0462 - val_accuracy: 0.6709
Epoch 15/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9964 - accuracy: 0.6831 - val_loss: 1.0459 - val_accuracy: 0.6709
Epoch 16/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9922 - accuracy: 0.6840 - val_loss: 1.0444 - val_accuracy: 0.6704
Epoch 17/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9884 - accuracy: 0.6848 - val_loss: 1.0405 - val_accuracy: 0.6725
Epoch 18/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9846 - accuracy: 0.6859 - val_loss: 1.0400 - val_accuracy: 0.6722
Epoch 19/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9822 - accuracy: 0.6864 - val_loss: 1.0394 - val_accuracy: 0.6728
Epoch 20/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9787 - accuracy: 0.6872 - val_loss: 1.0393 - val_accuracy: 0.6717
Epoch 21/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9761 - accuracy: 0.6878 - val_loss: 1.0398 - val_accuracy: 0.6725
Epoch 22/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9733 - accuracy: 0.6884 - val_loss: 1.0376 - val_accuracy: 0.6726
Epoch 23/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9708 - accuracy: 0.6890 - val_loss: 1.0352 - val_accuracy: 0.6732
Epoch 24/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9685 - accuracy: 0.6894 - val_loss: 1.0369 - val_accuracy: 0.6723
Epoch 25/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9660 - accuracy: 0.6901 - val_loss: 1.0384 - val_accuracy: 0.6733
Epoch 26/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9638 - accuracy: 0.6908 - val_loss: 1.0355 - val_accuracy: 0.6728
Epoch 27/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9619 - accuracy: 0.6912 - val_loss: 1.0325 - val_accuracy: 0.6739
Epoch 28/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9594 - accuracy: 0.6917 - val_loss: 1.0334 - val_accuracy: 0.6736
Epoch 29/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9582 - accuracy: 0.6920 - val_loss: 1.0366 - val_accuracy: 0.6733
Epoch 30/30
422/422 [==============================] - 3s 7ms/step - loss: 0.9561 - accuracy: 0.6926 - val_loss: 1.0336 - val_accuracy: 0.6728
<tensorflow.python.keras.callbacks.History at 0x7f95838ef750>우리는 더 많은 트레이닝과 하이퍼파라미터 튜닝을 통해 이러한 성능을 개선할 수 있습니다.
코드북 샘플링
이제 PixelCNN이 트레이닝되었으므로, 그 출력에서 고유한 코드를 샘플링하고 이를 디코더에 전달하여 새로운 이미지를 생성할 수 있습니다.
# 미니 샘플러 모델 생성
inputs = layers.Input(shape=pixel_cnn.input_shape[1:])
outputs = pixel_cnn(inputs, training=False)
categorical_layer = tfp.layers.DistributionLambda(tfp.distributions.Categorical)
outputs = categorical_layer(outputs)
sampler = keras.Model(inputs, outputs)이제 이미지를 생성하기 위한 사전 모델(prior)을 구성합니다. 여기서는 10개의 이미지를 생성할 것입니다.
# 비어있는 사전(priors)의 배열을 생성합니다.
batch = 10
priors = np.zeros(shape=(batch,) + (pixel_cnn.input_shape)[1:])
batch, rows, cols = priors.shape
# priors에 걸쳐 반복합니다. 생성은 픽셀별로 순차적으로 이루어져야 하기 때문입니다.
for row in range(rows):
for col in range(cols):
# 전체 배열을 입력하고, 다음 픽셀에 대한 픽셀 값 확률을 반환합니다.
probs = sampler.predict(priors)
# 확률을 사용하여 픽셀 값을 선택하고 사전(priors)에 값을 추가합니다.
priors[:, row, col] = probs[:, row, col]
print(f"Prior shape: {priors.shape}")결과
Prior shape: (10, 7, 7)이제 디코더를 사용하여 이미지를 생성할 수 있습니다.
# 임베딩 룩업 수행
pretrained_embeddings = quantizer.embeddings
priors_ohe = tf.one_hot(priors.astype("int32"), vqvae_trainer.num_embeddings).numpy()
quantized = tf.matmul(
priors_ohe.astype("float32"), pretrained_embeddings, transpose_b=True
)
quantized = tf.reshape(quantized, (-1, *(encoded_outputs.shape[1:])))
# 새로운(novel) 이미지 생성
decoder = vqvae_trainer.vqvae.get_layer("decoder")
generated_samples = decoder.predict(quantized)
for i in range(batch):
plt.subplot(1, 2, 1)
plt.imshow(priors[i])
plt.title("Code")
plt.axis("off")
plt.subplot(1, 2, 2)
plt.imshow(generated_samples[i].squeeze() + 0.5)
plt.title("Generated Sample")
plt.axis("off")
plt.show()
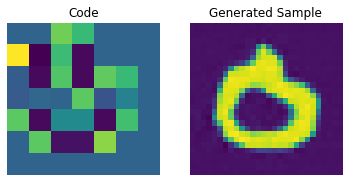
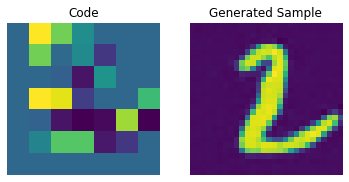
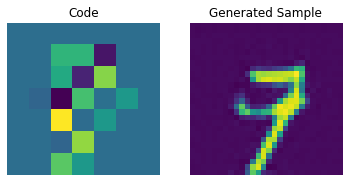
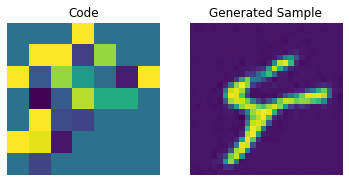
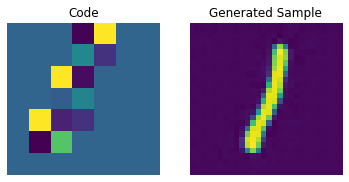
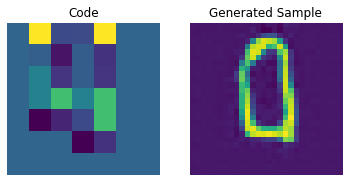
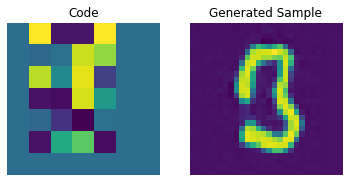
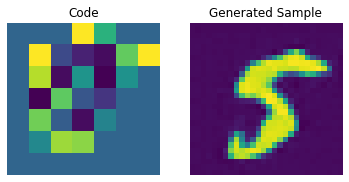

우리는 PixelCNN을 조정하여 생성된 샘플의 품질을 향상시킬 수 있습니다.