Visualize the hyperparameter tuning process
- Original Link : https://keras.io/guides/keras_tuner/visualize_tuning/
- Last Checked at : 2024-11-19
Author: Haifeng Jin
Date created: 2021/06/25
Last modified: 2021/06/05
Description: Using TensorBoard to visualize the hyperparameter tuning process in KerasTuner.
!pip install keras-tuner -qIntroduction
KerasTuner prints the logs to screen including the values of the hyperparameters in each trial for the user to monitor the progress. However, reading the logs is not intuitive enough to sense the influences of hyperparameters have on the results, Therefore, we provide a method to visualize the hyperparameter values and the corresponding evaluation results with interactive figures using TensorBoard.
TensorBoard is a useful tool for visualizing the machine learning experiments. It can monitor the losses and metrics during the model training and visualize the model architectures. Running KerasTuner with TensorBoard will give you additional features for visualizing hyperparameter tuning results using its HParams plugin.
We will use a simple example of tuning a model for the MNIST image classification dataset to show how to use KerasTuner with TensorBoard.
The first step is to download and format the data.
import numpy as np
import keras_tuner
import keras
from keras import layers
(x_train, y_train), (x_test, y_test) = keras.datasets.mnist.load_data()
# Normalize the pixel values to the range of [0, 1].
x_train = x_train.astype("float32") / 255
x_test = x_test.astype("float32") / 255
# Add the channel dimension to the images.
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)
# Print the shapes of the data.
print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)Result
(60000, 28, 28, 1)
(60000,)
(10000, 28, 28, 1)
(10000,)Then, we write a build_model function to build the model with hyperparameters and return the model. The hyperparameters include the type of model to use (multi-layer perceptron or convolutional neural network), the number of layers, the number of units or filters, whether to use dropout.
def build_model(hp):
inputs = keras.Input(shape=(28, 28, 1))
# Model type can be MLP or CNN.
model_type = hp.Choice("model_type", ["mlp", "cnn"])
x = inputs
if model_type == "mlp":
x = layers.Flatten()(x)
# Number of layers of the MLP is a hyperparameter.
for i in range(hp.Int("mlp_layers", 1, 3)):
# Number of units of each layer are
# different hyperparameters with different names.
x = layers.Dense(
units=hp.Int(f"units_{i}", 32, 128, step=32),
activation="relu",
)(x)
else:
# Number of layers of the CNN is also a hyperparameter.
for i in range(hp.Int("cnn_layers", 1, 3)):
x = layers.Conv2D(
hp.Int(f"filters_{i}", 32, 128, step=32),
kernel_size=(3, 3),
activation="relu",
)(x)
x = layers.MaxPooling2D(pool_size=(2, 2))(x)
x = layers.Flatten()(x)
# A hyperparamter for whether to use dropout layer.
if hp.Boolean("dropout"):
x = layers.Dropout(0.5)(x)
# The last layer contains 10 units,
# which is the same as the number of classes.
outputs = layers.Dense(units=10, activation="softmax")(x)
model = keras.Model(inputs=inputs, outputs=outputs)
# Compile the model.
model.compile(
loss="sparse_categorical_crossentropy",
metrics=["accuracy"],
optimizer="adam",
)
return modelWe can do a quick test of the models to check if it build successfully for both CNN and MLP.
# Initialize the `HyperParameters` and set the values.
hp = keras_tuner.HyperParameters()
hp.values["model_type"] = "cnn"
# Build the model using the `HyperParameters`.
model = build_model(hp)
# Test if the model runs with our data.
model(x_train[:100])
# Print a summary of the model.
model.summary()
# Do the same for MLP model.
hp.values["model_type"] = "mlp"
model = build_model(hp)
model(x_train[:100])
model.summary()Result
Model: "functional_1"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━┩
│ input_layer (InputLayer) │ (None, 28, 28, 1) │ 0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ conv2d (Conv2D) │ (None, 26, 26, 32) │ 320 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ max_pooling2d (MaxPooling2D) │ (None, 13, 13, 32) │ 0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ flatten (Flatten) │ (None, 5408) │ 0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ dense (Dense) │ (None, 10) │ 54,090 │
└─────────────────────────────────┴───────────────────────────┴────────────┘
Total params: 54,410 (212.54 KB)
Trainable params: 54,410 (212.54 KB)
Non-trainable params: 0 (0.00 B)
Model: "functional_3"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━┩
│ input_layer_1 (InputLayer) │ (None, 28, 28, 1) │ 0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ flatten_1 (Flatten) │ (None, 784) │ 0 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ dense_1 (Dense) │ (None, 32) │ 25,120 │
├─────────────────────────────────┼───────────────────────────┼────────────┤
│ dense_2 (Dense) │ (None, 10) │ 330 │
└─────────────────────────────────┴───────────────────────────┴────────────┘
Total params: 25,450 (99.41 KB)
Trainable params: 25,450 (99.41 KB)
Non-trainable params: 0 (0.00 B)Initialize the RandomSearch tuner with 10 trials and using validation accuracy as the metric for selecting models.
tuner = keras_tuner.RandomSearch(
build_model,
max_trials=10,
# Do not resume the previous search in the same directory.
overwrite=True,
objective="val_accuracy",
# Set a directory to store the intermediate results.
directory="/tmp/tb",
)Start the search by calling tuner.search(...). To use TensorBoard, we need to pass a keras.callbacks.TensorBoard instance to the callbacks.
tuner.search(
x_train,
y_train,
validation_split=0.2,
epochs=2,
# Use the TensorBoard callback.
# The logs will be write to "/tmp/tb_logs".
callbacks=[keras.callbacks.TensorBoard("/tmp/tb_logs")],
)Result
Trial 10 Complete [00h 00m 06s]
val_accuracy: 0.9617499709129333Best val_accuracy So Far: 0.9837499856948853
Total elapsed time: 00h 08m 32sIf running in Colab, the following two commands will show you the TensorBoard inside Colab.
%load_ext tensorboard
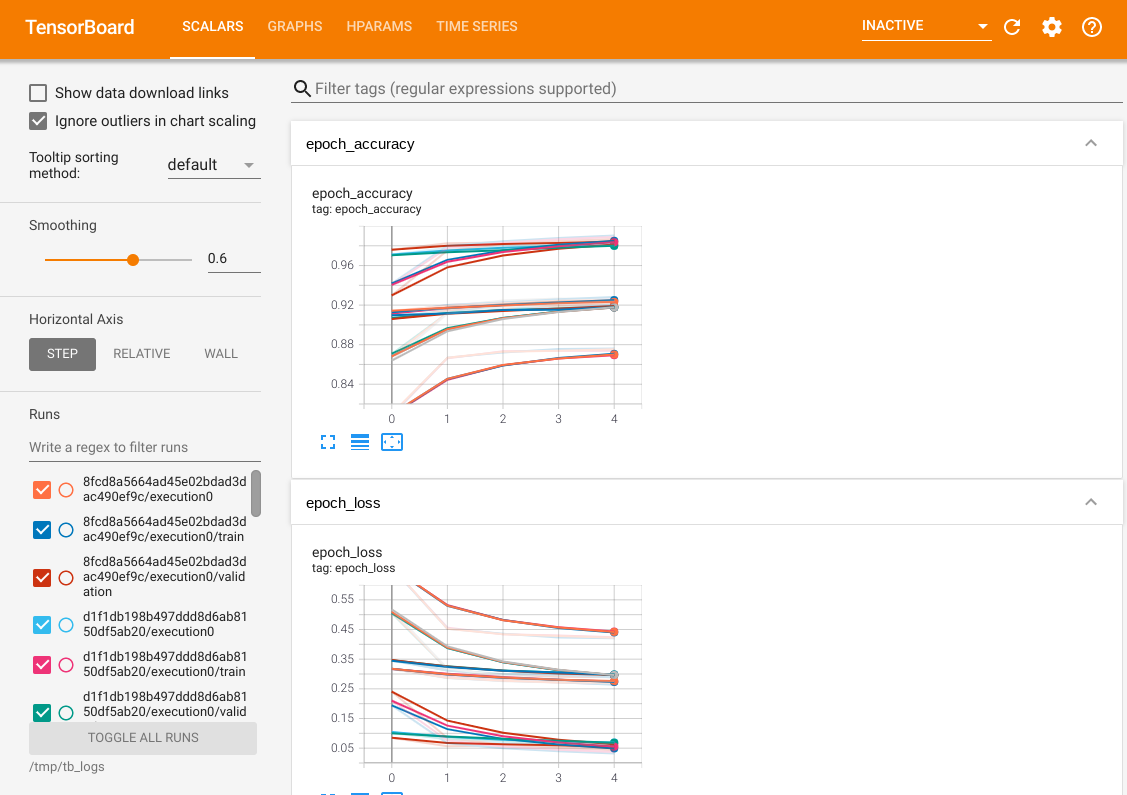
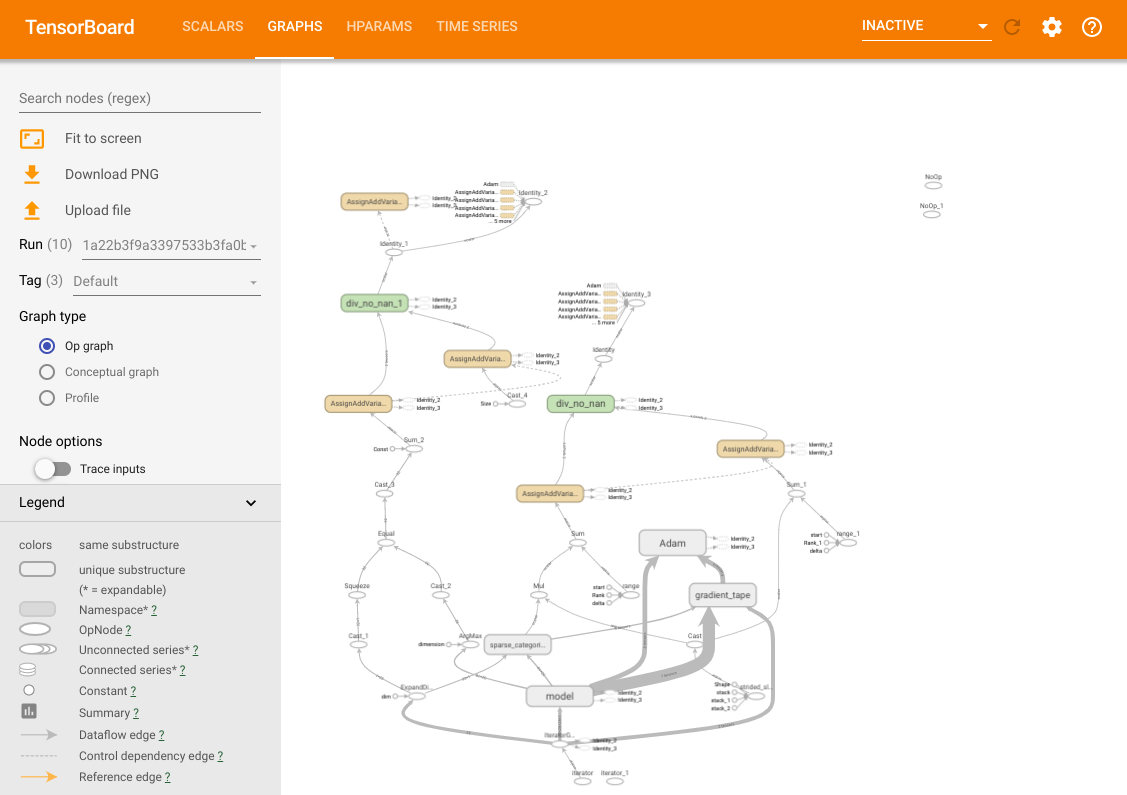
%tensorboard --logdir /tmp/tb_logsYou have access to all the common features of the TensorBoard. For example, you can view the loss and metrics curves and visualize the computational graph of the models in different trials.
In addition to these features, we also have a HParams tab, in which there are three views. In the table view, you can view the 10 different trials in a table with the different hyperparameter values and evaluation metrics.
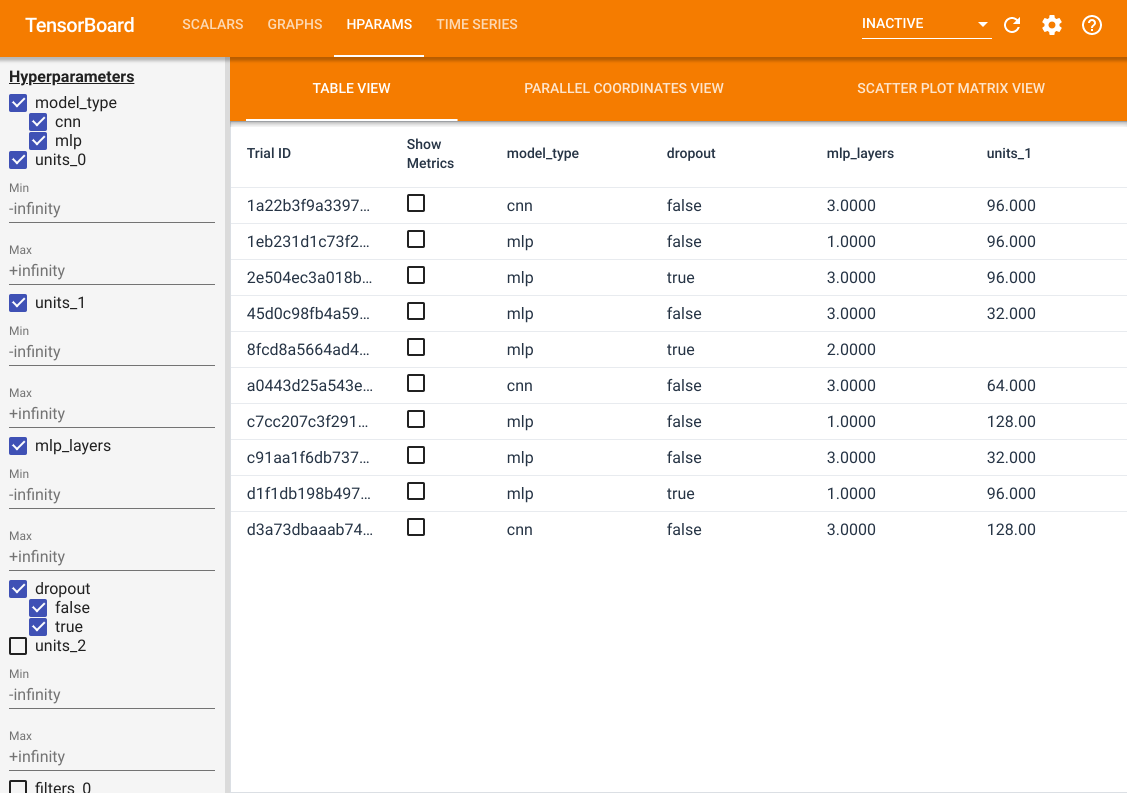
On the left side, you can specify the filters for certain hyperparameters. For example, you can specify to only view the MLP models without the dropout layer and with 1 to 2 dense layers.
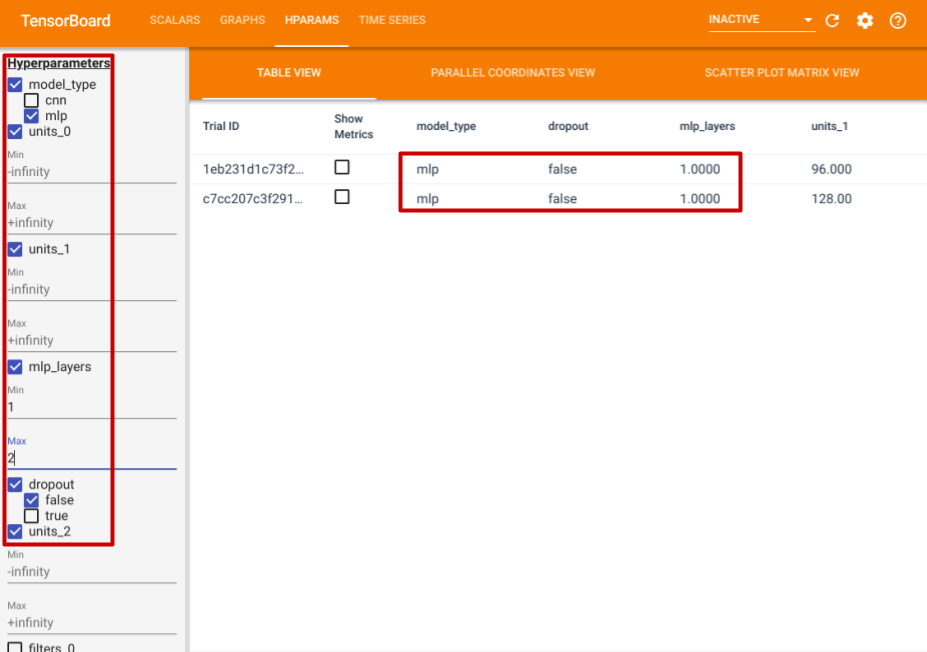
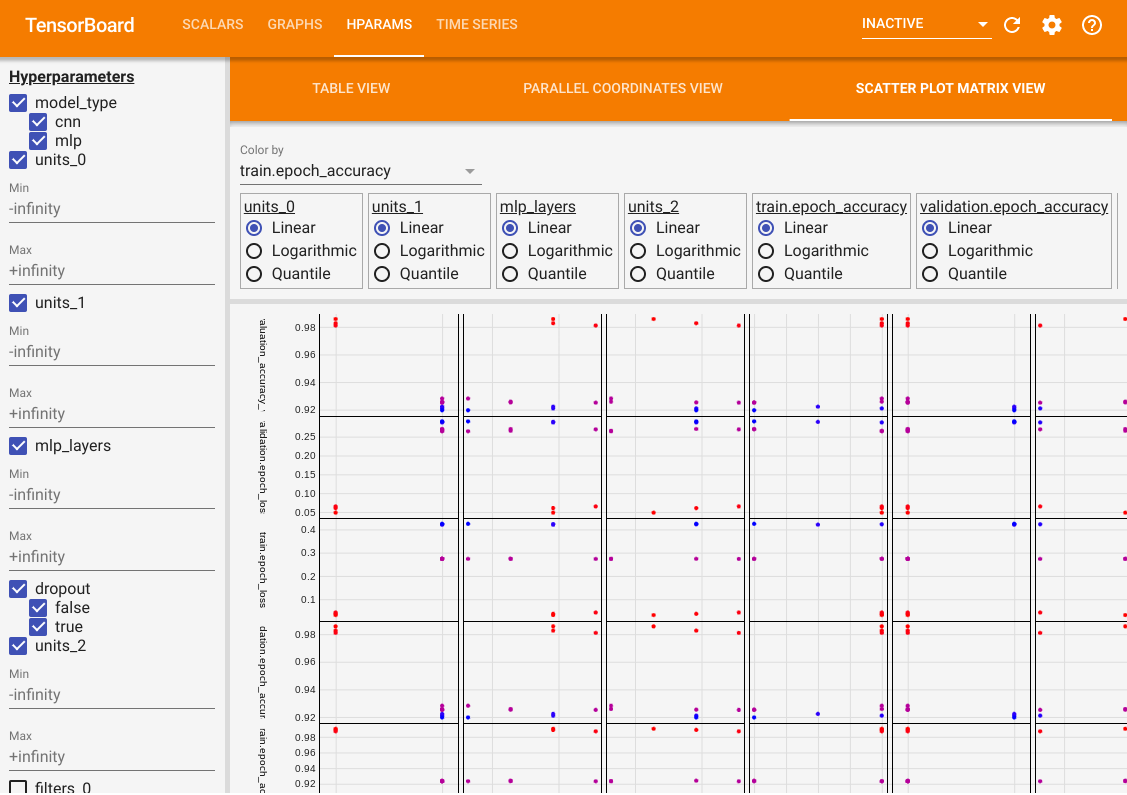
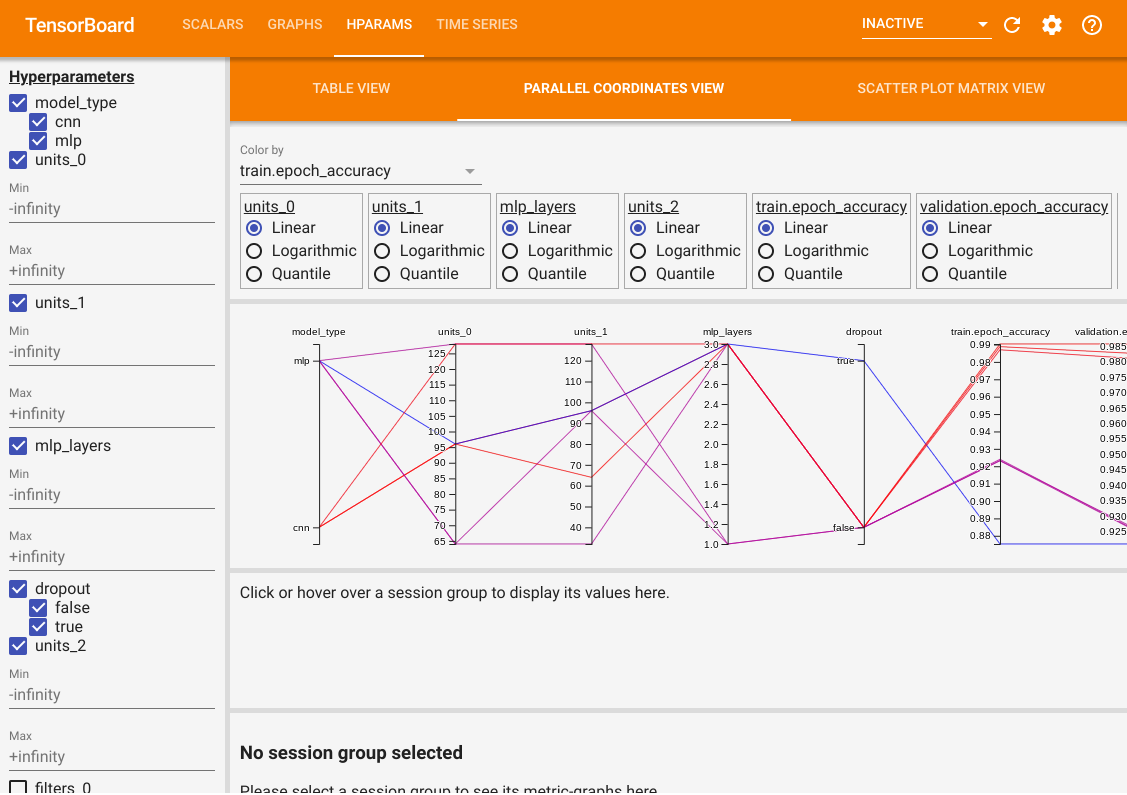
Besides the table view, it also provides two other views, parallel coordinates view and scatter plot matrix view. They are just different visualization methods for the same data. You can still use the panel on the left to filter the results.
In the parallel coordinates view, each colored line is a trial. The axes are the hyperparameters and evaluation metrics.
In the scatter plot matrix view, each dot is a trial. The plots are projections of the trials on planes with different hyperparameter and metrics as the axes.