Structured data learning with Wide, Deep, and Cross networks
- Original Link : https://keras.io/examples/structured_data/wide_deep_cross_networks/
- Last Checked at : 2024-11-22
Author: Khalid Salama
Date created: 2020/12/31
Last modified: 2021/05/05
Description: Using Wide & Deep and Deep & Cross networks for structured data classification.
Introduction
This example demonstrates how to do structured data classification using the two modeling techniques:
- Wide & Deep models
- Deep & Cross models
Note that this example should be run with TensorFlow 2.5 or higher.
The dataset
This example uses the Covertype dataset from the UCI Machine Learning Repository. The task is to predict forest cover type from cartographic variables. The dataset includes 506,011 instances with 12 input features: 10 numerical features and 2 categorical features. Each instance is categorized into 1 of 7 classes.
Setup
import os
# Only the TensorFlow backend supports string inputs.
os.environ["KERAS_BACKEND"] = "tensorflow"
import math
import numpy as np
import pandas as pd
from tensorflow import data as tf_data
import keras
from keras import layersPrepare the data
First, let’s load the dataset from the UCI Machine Learning Repository into a Pandas DataFrame:
data_url = (
"https://archive.ics.uci.edu/ml/machine-learning-databases/covtype/covtype.data.gz"
)
raw_data = pd.read_csv(data_url, header=None)
print(f"Dataset shape: {raw_data.shape}")
raw_data.head()Result
Dataset shape: (581012, 55)| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … | 45 | 46 | 47 | 48 | 49 | 50 | 51 | 52 | 53 | 54 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2596 | 51 | 3 | 258 | 0 | 510 | 221 | 232 | 148 | 6279 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| 1 | 2590 | 56 | 2 | 212 | -6 | 390 | 220 | 235 | 151 | 6225 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
| 2 | 2804 | 139 | 9 | 268 | 65 | 3180 | 234 | 238 | 135 | 6121 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| 3 | 2785 | 155 | 18 | 242 | 118 | 3090 | 238 | 238 | 122 | 6211 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| 4 | 2595 | 45 | 2 | 153 | -1 | 391 | 220 | 234 | 150 | 6172 | … | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5 |
5 rows × 55 columns
The two categorical features in the dataset are binary-encoded. We will convert this dataset representation to the typical representation, where each categorical feature is represented as a single integer value.
soil_type_values = [f"soil_type_{idx+1}" for idx in range(40)]
wilderness_area_values = [f"area_type_{idx+1}" for idx in range(4)]
soil_type = raw_data.loc[:, 14:53].apply(
lambda x: soil_type_values[0::1][x.to_numpy().nonzero()[0][0]], axis=1
)
wilderness_area = raw_data.loc[:, 10:13].apply(
lambda x: wilderness_area_values[0::1][x.to_numpy().nonzero()[0][0]], axis=1
)
CSV_HEADER = [
"Elevation",
"Aspect",
"Slope",
"Horizontal_Distance_To_Hydrology",
"Vertical_Distance_To_Hydrology",
"Horizontal_Distance_To_Roadways",
"Hillshade_9am",
"Hillshade_Noon",
"Hillshade_3pm",
"Horizontal_Distance_To_Fire_Points",
"Wilderness_Area",
"Soil_Type",
"Cover_Type",
]
data = pd.concat(
[raw_data.loc[:, 0:9], wilderness_area, soil_type, raw_data.loc[:, 54]],
axis=1,
ignore_index=True,
)
data.columns = CSV_HEADER
# Convert the target label indices into a range from 0 to 6 (there are 7 labels in total).
data["Cover_Type"] = data["Cover_Type"] - 1
print(f"Dataset shape: {data.shape}")
data.head().TResult
Dataset shape: (581012, 13)| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Elevation | 2596 | 2590 | 2804 | 2785 | 2595 |
| Aspect | 51 | 56 | 139 | 155 | 45 |
| Slope | 3 | 2 | 9 | 18 | 2 |
| Horizontal_Distance_To_Hydrology | 258 | 212 | 268 | 242 | 153 |
| Vertical_Distance_To_Hydrology | 0 | -6 | 65 | 118 | -1 |
| Horizontal_Distance_To_Roadways | 510 | 390 | 3180 | 3090 | 391 |
| Hillshade_9am | 221 | 220 | 234 | 238 | 220 |
| Hillshade_Noon | 232 | 235 | 238 | 238 | 234 |
| Hillshade_3pm | 148 | 151 | 135 | 122 | 150 |
| Horizontal_Distance_To_Fire_Points | 6279 | 6225 | 6121 | 6211 | 6172 |
| Wilderness_Area | area_type_1 | area_type_1 | area_type_1 | area_type_1 | area_type_1 |
| Soil_Type | soil_type_29 | soil_type_29 | soil_type_12 | soil_type_30 | soil_type_29 |
| Cover_Type | 4 | 4 | 1 | 1 | 4 |
The shape of the DataFrame shows there are 13 columns per sample (12 for the features and 1 for the target label).
Let’s split the data into training (85%) and test (15%) sets.
train_splits = []
test_splits = []
for _, group_data in data.groupby("Cover_Type"):
random_selection = np.random.rand(len(group_data.index)) <= 0.85
train_splits.append(group_data[random_selection])
test_splits.append(group_data[~random_selection])
train_data = pd.concat(train_splits).sample(frac=1).reset_index(drop=True)
test_data = pd.concat(test_splits).sample(frac=1).reset_index(drop=True)
print(f"Train split size: {len(train_data.index)}")
print(f"Test split size: {len(test_data.index)}")Result
Train split size: 493323
Test split size: 87689Next, store the training and test data in separate CSV files.
train_data_file = "train_data.csv"
test_data_file = "test_data.csv"
train_data.to_csv(train_data_file, index=False)
test_data.to_csv(test_data_file, index=False)Define dataset metadata
Here, we define the metadata of the dataset that will be useful for reading and parsing the data into input features, and encoding the input features with respect to their types.
TARGET_FEATURE_NAME = "Cover_Type"
TARGET_FEATURE_LABELS = ["0", "1", "2", "3", "4", "5", "6"]
NUMERIC_FEATURE_NAMES = [
"Aspect",
"Elevation",
"Hillshade_3pm",
"Hillshade_9am",
"Hillshade_Noon",
"Horizontal_Distance_To_Fire_Points",
"Horizontal_Distance_To_Hydrology",
"Horizontal_Distance_To_Roadways",
"Slope",
"Vertical_Distance_To_Hydrology",
]
CATEGORICAL_FEATURES_WITH_VOCABULARY = {
"Soil_Type": list(data["Soil_Type"].unique()),
"Wilderness_Area": list(data["Wilderness_Area"].unique()),
}
CATEGORICAL_FEATURE_NAMES = list(CATEGORICAL_FEATURES_WITH_VOCABULARY.keys())
FEATURE_NAMES = NUMERIC_FEATURE_NAMES + CATEGORICAL_FEATURE_NAMES
COLUMN_DEFAULTS = [
[0] if feature_name in NUMERIC_FEATURE_NAMES + [TARGET_FEATURE_NAME] else ["NA"]
for feature_name in CSV_HEADER
]
NUM_CLASSES = len(TARGET_FEATURE_LABELS)Experiment setup
Next, let’s define an input function that reads and parses the file, then converts features and labels into atf.data.Dataset for training or evaluation.
def get_dataset_from_csv(csv_file_path, batch_size, shuffle=False):
dataset = tf_data.experimental.make_csv_dataset(
csv_file_path,
batch_size=batch_size,
column_names=CSV_HEADER,
column_defaults=COLUMN_DEFAULTS,
label_name=TARGET_FEATURE_NAME,
num_epochs=1,
header=True,
shuffle=shuffle,
)
return dataset.cache()Here we configure the parameters and implement the procedure for running a training and evaluation experiment given a model.
learning_rate = 0.001
dropout_rate = 0.1
batch_size = 265
num_epochs = 50
hidden_units = [32, 32]
def run_experiment(model):
model.compile(
optimizer=keras.optimizers.Adam(learning_rate=learning_rate),
loss=keras.losses.SparseCategoricalCrossentropy(),
metrics=[keras.metrics.SparseCategoricalAccuracy()],
)
train_dataset = get_dataset_from_csv(train_data_file, batch_size, shuffle=True)
test_dataset = get_dataset_from_csv(test_data_file, batch_size)
print("Start training the model...")
history = model.fit(train_dataset, epochs=num_epochs)
print("Model training finished")
_, accuracy = model.evaluate(test_dataset, verbose=0)
print(f"Test accuracy: {round(accuracy * 100, 2)}%")Create model inputs
Now, define the inputs for the models as a dictionary, where the key is the feature name, and the value is a keras.layers.Input tensor with the corresponding feature shape and data type.
def create_model_inputs():
inputs = {}
for feature_name in FEATURE_NAMES:
if feature_name in NUMERIC_FEATURE_NAMES:
inputs[feature_name] = layers.Input(
name=feature_name, shape=(), dtype="float32"
)
else:
inputs[feature_name] = layers.Input(
name=feature_name, shape=(), dtype="string"
)
return inputsEncode features
We create two representations of our input features: sparse and dense: 1. In the sparse representation, the categorical features are encoded with one-hot encoding using the CategoryEncoding layer. This representation can be useful for the model to memorize particular feature values to make certain predictions. 2. In the dense representation, the categorical features are encoded with low-dimensional embeddings using the Embedding layer. This representation helps the model to generalize well to unseen feature combinations.
def encode_inputs(inputs, use_embedding=False):
encoded_features = []
for feature_name in inputs:
if feature_name in CATEGORICAL_FEATURE_NAMES:
vocabulary = CATEGORICAL_FEATURES_WITH_VOCABULARY[feature_name]
# Create a lookup to convert string values to an integer indices.
# Since we are not using a mask token nor expecting any out of vocabulary
# (oov) token, we set mask_token to None and num_oov_indices to 0.
lookup = layers.StringLookup(
vocabulary=vocabulary,
mask_token=None,
num_oov_indices=0,
output_mode="int" if use_embedding else "binary",
)
if use_embedding:
# Convert the string input values into integer indices.
encoded_feature = lookup(inputs[feature_name])
embedding_dims = int(math.sqrt(len(vocabulary)))
# Create an embedding layer with the specified dimensions.
embedding = layers.Embedding(
input_dim=len(vocabulary), output_dim=embedding_dims
)
# Convert the index values to embedding representations.
encoded_feature = embedding(encoded_feature)
else:
# Convert the string input values into a one hot encoding.
encoded_feature = lookup(
keras.ops.expand_dims(inputs[feature_name], -1)
)
else:
# Use the numerical features as-is.
encoded_feature = keras.ops.expand_dims(inputs[feature_name], -1)
encoded_features.append(encoded_feature)
all_features = layers.concatenate(encoded_features)
return all_featuresExperiment 1: a baseline model
In the first experiment, let’s create a multi-layer feed-forward network, where the categorical features are one-hot encoded.
def create_baseline_model():
inputs = create_model_inputs()
features = encode_inputs(inputs)
for units in hidden_units:
features = layers.Dense(units)(features)
features = layers.BatchNormalization()(features)
features = layers.ReLU()(features)
features = layers.Dropout(dropout_rate)(features)
outputs = layers.Dense(units=NUM_CLASSES, activation="softmax")(features)
model = keras.Model(inputs=inputs, outputs=outputs)
return model
baseline_model = create_baseline_model()
keras.utils.plot_model(baseline_model, show_shapes=True, rankdir="LR")Result
/Users/fchollet/Library/Python/3.10/lib/python/site-packages/numpy/core/numeric.py:2468: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison
return bool(asarray(a1 == a2).all())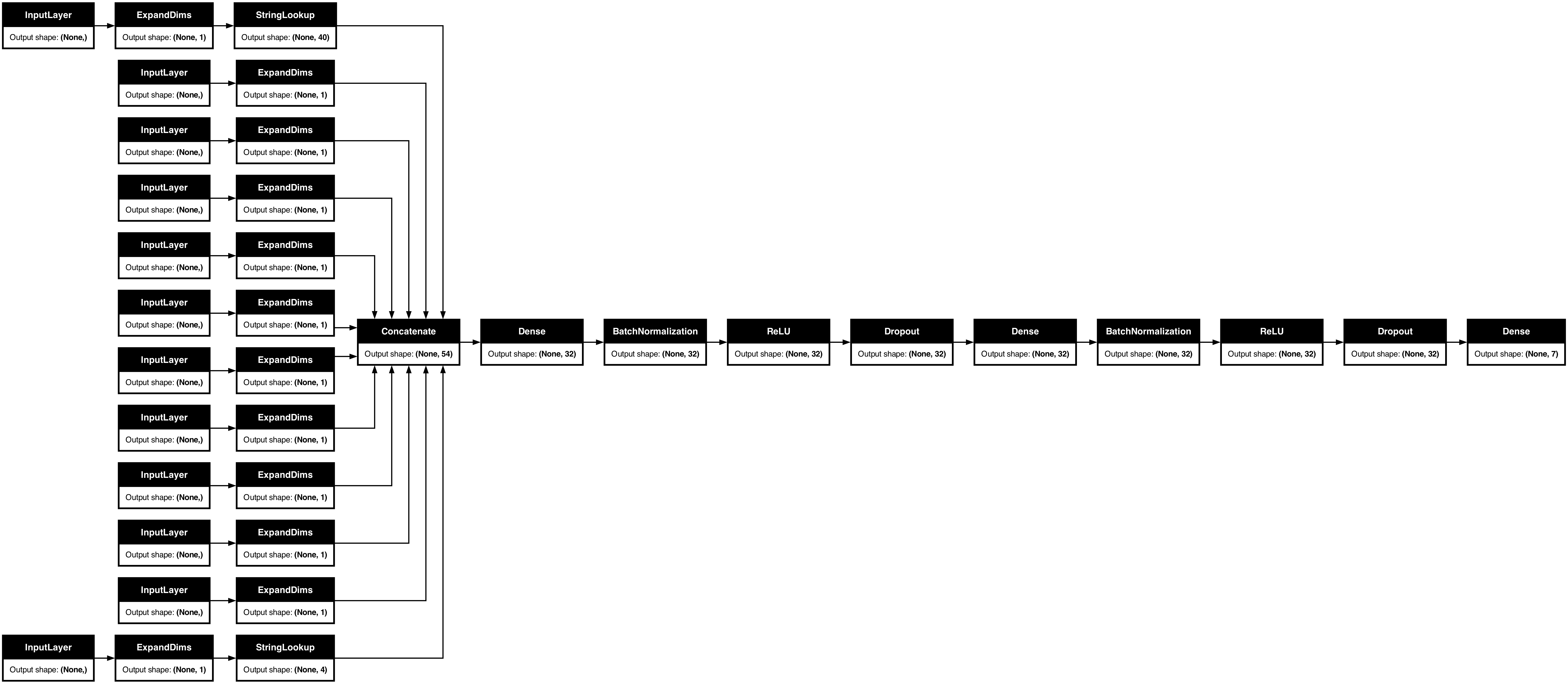
Let’s run it:
run_experiment(baseline_model)Result
Start training the model...
Epoch 1/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 6s 3ms/step - loss: 1.0713 - sparse_categorical_accuracy: 0.5634
Epoch 2/50
179/1862 ━[37m━━━━━━━━━━━━━━━━━━━ 1s 848us/step - loss: 0.7473 - sparse_categorical_accuracy: 0.6840
/Library/Frameworks/Python.framework/Versions/3.10/lib/python3.10/contextlib.py:153: UserWarning: Your input ran out of data; interrupting training. Make sure that your dataset or generator can generate at least `steps_per_epoch * epochs` batches. You may need to use the `.repeat()` function when building your dataset.
self.gen.throw(typ, value, traceback)
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 904us/step - loss: 0.7386 - sparse_categorical_accuracy: 0.6866
Epoch 3/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 909us/step - loss: 0.7135 - sparse_categorical_accuracy: 0.6958
Epoch 4/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 878us/step - loss: 0.6975 - sparse_categorical_accuracy: 0.7051
Epoch 5/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 941us/step - loss: 0.6876 - sparse_categorical_accuracy: 0.7089
Epoch 6/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 936us/step - loss: 0.6848 - sparse_categorical_accuracy: 0.7106
Epoch 7/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 934us/step - loss: 0.7165 - sparse_categorical_accuracy: 0.6969
Epoch 8/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 924us/step - loss: 0.6979 - sparse_categorical_accuracy: 0.7053
Epoch 9/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 967us/step - loss: 0.6913 - sparse_categorical_accuracy: 0.7088
Epoch 10/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 975us/step - loss: 0.6807 - sparse_categorical_accuracy: 0.7124
Epoch 11/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 987us/step - loss: 0.6829 - sparse_categorical_accuracy: 0.7110
Epoch 12/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 917us/step - loss: 0.6823 - sparse_categorical_accuracy: 0.7109
Epoch 13/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 879us/step - loss: 0.6658 - sparse_categorical_accuracy: 0.7175
Epoch 14/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 948us/step - loss: 0.6677 - sparse_categorical_accuracy: 0.7170
Epoch 15/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 866us/step - loss: 0.6695 - sparse_categorical_accuracy: 0.7130
Epoch 16/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 860us/step - loss: 0.6847 - sparse_categorical_accuracy: 0.7074
Epoch 17/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 853us/step - loss: 0.6660 - sparse_categorical_accuracy: 0.7174
Epoch 18/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 855us/step - loss: 0.6620 - sparse_categorical_accuracy: 0.7184
Epoch 19/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 900us/step - loss: 0.6642 - sparse_categorical_accuracy: 0.7163
Epoch 20/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 969us/step - loss: 0.6614 - sparse_categorical_accuracy: 0.7167
Epoch 21/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 988us/step - loss: 0.6560 - sparse_categorical_accuracy: 0.7199
Epoch 22/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 969us/step - loss: 0.6559 - sparse_categorical_accuracy: 0.7201
Epoch 23/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 868us/step - loss: 0.6514 - sparse_categorical_accuracy: 0.7217
Epoch 24/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 925us/step - loss: 0.6509 - sparse_categorical_accuracy: 0.7222
Epoch 25/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 879us/step - loss: 0.6464 - sparse_categorical_accuracy: 0.7233
Epoch 26/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 898us/step - loss: 0.6442 - sparse_categorical_accuracy: 0.7237
Epoch 27/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 842us/step - loss: 0.6476 - sparse_categorical_accuracy: 0.7210
Epoch 28/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 815us/step - loss: 0.6427 - sparse_categorical_accuracy: 0.7247
Epoch 29/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 837us/step - loss: 0.6414 - sparse_categorical_accuracy: 0.7244
Epoch 30/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 865us/step - loss: 0.6408 - sparse_categorical_accuracy: 0.7256
Epoch 31/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 845us/step - loss: 0.6378 - sparse_categorical_accuracy: 0.7269
Epoch 32/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 842us/step - loss: 0.6432 - sparse_categorical_accuracy: 0.7235
Epoch 33/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 905us/step - loss: 0.6482 - sparse_categorical_accuracy: 0.7226
Epoch 34/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.6586 - sparse_categorical_accuracy: 0.7191
Epoch 35/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 958us/step - loss: 0.6511 - sparse_categorical_accuracy: 0.7215
Epoch 36/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 910us/step - loss: 0.6571 - sparse_categorical_accuracy: 0.7217
Epoch 37/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 897us/step - loss: 0.6451 - sparse_categorical_accuracy: 0.7253
Epoch 38/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 846us/step - loss: 0.6455 - sparse_categorical_accuracy: 0.7254
Epoch 39/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 907us/step - loss: 0.6722 - sparse_categorical_accuracy: 0.7131
Epoch 40/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1000us/step - loss: 0.6393 - sparse_categorical_accuracy: 0.7282
Epoch 41/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 872us/step - loss: 0.6804 - sparse_categorical_accuracy: 0.7078
Epoch 42/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 884us/step - loss: 0.6657 - sparse_categorical_accuracy: 0.7135
Epoch 43/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 960us/step - loss: 0.6557 - sparse_categorical_accuracy: 0.7180
Epoch 44/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 870us/step - loss: 0.6671 - sparse_categorical_accuracy: 0.7115
Epoch 45/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 871us/step - loss: 0.6730 - sparse_categorical_accuracy: 0.7069
Epoch 46/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 875us/step - loss: 0.6669 - sparse_categorical_accuracy: 0.7105
Epoch 47/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 847us/step - loss: 0.6634 - sparse_categorical_accuracy: 0.7129
Epoch 48/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 846us/step - loss: 0.6625 - sparse_categorical_accuracy: 0.7137
Epoch 49/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 824us/step - loss: 0.6596 - sparse_categorical_accuracy: 0.7146
Epoch 50/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 833us/step - loss: 0.6714 - sparse_categorical_accuracy: 0.7106
Model training finished
Test accuracy: 69.5%The baseline linear model achieves ~76% test accuracy.
Experiment 2: Wide & Deep model
In the second experiment, we create a Wide & Deep model. The wide part of the model a linear model, while the deep part of the model is a multi-layer feed-forward network.
Use the sparse representation of the input features in the wide part of the model and the dense representation of the input features for the deep part of the model.
Note that every input features contributes to both parts of the model with different representations.
def create_wide_and_deep_model():
inputs = create_model_inputs()
wide = encode_inputs(inputs)
wide = layers.BatchNormalization()(wide)
deep = encode_inputs(inputs, use_embedding=True)
for units in hidden_units:
deep = layers.Dense(units)(deep)
deep = layers.BatchNormalization()(deep)
deep = layers.ReLU()(deep)
deep = layers.Dropout(dropout_rate)(deep)
merged = layers.concatenate([wide, deep])
outputs = layers.Dense(units=NUM_CLASSES, activation="softmax")(merged)
model = keras.Model(inputs=inputs, outputs=outputs)
return model
wide_and_deep_model = create_wide_and_deep_model()
keras.utils.plot_model(wide_and_deep_model, show_shapes=True, rankdir="LR")Result
/Users/fchollet/Library/Python/3.10/lib/python/site-packages/numpy/core/numeric.py:2468: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison
return bool(asarray(a1 == a2).all())
Let’s run it:
run_experiment(wide_and_deep_model)Result
Start training the model...
Epoch 1/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 5s 2ms/step - loss: 0.8979 - sparse_categorical_accuracy: 0.6386
Epoch 2/50
128/1862 ━[37m━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.6317 - sparse_categorical_accuracy: 0.7302
/Library/Frameworks/Python.framework/Versions/3.10/lib/python3.10/contextlib.py:153: UserWarning: Your input ran out of data; interrupting training. Make sure that your dataset or generator can generate at least `steps_per_epoch * epochs` batches. You may need to use the `.repeat()` function when building your dataset.
self.gen.throw(typ, value, traceback)
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.6290 - sparse_categorical_accuracy: 0.7295
Epoch 3/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.6130 - sparse_categorical_accuracy: 0.7350
Epoch 4/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.6029 - sparse_categorical_accuracy: 0.7397
Epoch 5/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 3s 1ms/step - loss: 0.6010 - sparse_categorical_accuracy: 0.7397
Epoch 6/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5924 - sparse_categorical_accuracy: 0.7445
Epoch 7/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5917 - sparse_categorical_accuracy: 0.7442
Epoch 8/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5945 - sparse_categorical_accuracy: 0.7438
Epoch 9/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5933 - sparse_categorical_accuracy: 0.7443
Epoch 10/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5862 - sparse_categorical_accuracy: 0.7481
Epoch 11/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5809 - sparse_categorical_accuracy: 0.7507
Epoch 12/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5777 - sparse_categorical_accuracy: 0.7519
Epoch 13/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5736 - sparse_categorical_accuracy: 0.7534
Epoch 14/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5716 - sparse_categorical_accuracy: 0.7545
Epoch 15/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5736 - sparse_categorical_accuracy: 0.7537
Epoch 16/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5712 - sparse_categorical_accuracy: 0.7559
Epoch 17/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5683 - sparse_categorical_accuracy: 0.7564
Epoch 18/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5666 - sparse_categorical_accuracy: 0.7569
Epoch 19/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5652 - sparse_categorical_accuracy: 0.7575
Epoch 20/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5634 - sparse_categorical_accuracy: 0.7583
Epoch 21/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5677 - sparse_categorical_accuracy: 0.7563
Epoch 22/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5651 - sparse_categorical_accuracy: 0.7578
Epoch 23/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5628 - sparse_categorical_accuracy: 0.7586
Epoch 24/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5619 - sparse_categorical_accuracy: 0.7593
Epoch 25/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5603 - sparse_categorical_accuracy: 0.7589
Epoch 26/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5644 - sparse_categorical_accuracy: 0.7585
Epoch 27/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5592 - sparse_categorical_accuracy: 0.7604
Epoch 28/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5571 - sparse_categorical_accuracy: 0.7616
Epoch 29/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5556 - sparse_categorical_accuracy: 0.7629
Epoch 30/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5538 - sparse_categorical_accuracy: 0.7640
Epoch 31/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5535 - sparse_categorical_accuracy: 0.7635
Epoch 32/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5521 - sparse_categorical_accuracy: 0.7645
Epoch 33/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5505 - sparse_categorical_accuracy: 0.7648
Epoch 34/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5494 - sparse_categorical_accuracy: 0.7657
Epoch 35/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5496 - sparse_categorical_accuracy: 0.7660
Epoch 36/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5488 - sparse_categorical_accuracy: 0.7673
Epoch 37/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5471 - sparse_categorical_accuracy: 0.7668
Epoch 38/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5474 - sparse_categorical_accuracy: 0.7673
Epoch 39/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5457 - sparse_categorical_accuracy: 0.7674
Epoch 40/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5452 - sparse_categorical_accuracy: 0.7689
Epoch 41/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5448 - sparse_categorical_accuracy: 0.7679
Epoch 42/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 3s 1ms/step - loss: 0.5442 - sparse_categorical_accuracy: 0.7692
Epoch 43/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5436 - sparse_categorical_accuracy: 0.7701
Epoch 44/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5419 - sparse_categorical_accuracy: 0.7706
Epoch 45/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5432 - sparse_categorical_accuracy: 0.7691
Epoch 46/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5406 - sparse_categorical_accuracy: 0.7708
Epoch 47/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5412 - sparse_categorical_accuracy: 0.7701
Epoch 48/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5400 - sparse_categorical_accuracy: 0.7701
Epoch 49/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5416 - sparse_categorical_accuracy: 0.7699
Epoch 50/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5403 - sparse_categorical_accuracy: 0.7701
Model training finished
Test accuracy: 79.04%The wide and deep model achieves ~79% test accuracy.
Experiment 3: Deep & Cross model
In the third experiment, we create a Deep & Cross model. The deep part of this model is the same as the deep part created in the previous experiment. The key idea of the cross part is to apply explicit feature crossing in an efficient way, where the degree of cross features grows with layer depth.
def create_deep_and_cross_model():
inputs = create_model_inputs()
x0 = encode_inputs(inputs, use_embedding=True)
cross = x0
for _ in hidden_units:
units = cross.shape[-1]
x = layers.Dense(units)(cross)
cross = x0 * x + cross
cross = layers.BatchNormalization()(cross)
deep = x0
for units in hidden_units:
deep = layers.Dense(units)(deep)
deep = layers.BatchNormalization()(deep)
deep = layers.ReLU()(deep)
deep = layers.Dropout(dropout_rate)(deep)
merged = layers.concatenate([cross, deep])
outputs = layers.Dense(units=NUM_CLASSES, activation="softmax")(merged)
model = keras.Model(inputs=inputs, outputs=outputs)
return model
deep_and_cross_model = create_deep_and_cross_model()
keras.utils.plot_model(deep_and_cross_model, show_shapes=True, rankdir="LR")Result
/Users/fchollet/Library/Python/3.10/lib/python/site-packages/numpy/core/numeric.py:2468: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison
return bool(asarray(a1 == a2).all())
Let’s run it:
run_experiment(deep_and_cross_model)Result
Start training the model...
Epoch 1/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 5s 2ms/step - loss: 0.9221 - sparse_categorical_accuracy: 0.6235
Epoch 2/50
116/1862 ━[37m━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.6388 - sparse_categorical_accuracy: 0.7257
/Library/Frameworks/Python.framework/Versions/3.10/lib/python3.10/contextlib.py:153: UserWarning: Your input ran out of data; interrupting training. Make sure that your dataset or generator can generate at least `steps_per_epoch * epochs` batches. You may need to use the `.repeat()` function when building your dataset.
self.gen.throw(typ, value, traceback)
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - loss: 0.6271 - sparse_categorical_accuracy: 0.7316
Epoch 3/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 3s 1ms/step - loss: 0.6023 - sparse_categorical_accuracy: 0.7403
Epoch 4/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5896 - sparse_categorical_accuracy: 0.7453
Epoch 5/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5899 - sparse_categorical_accuracy: 0.7438
Epoch 6/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5960 - sparse_categorical_accuracy: 0.7421
Epoch 7/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5813 - sparse_categorical_accuracy: 0.7481
Epoch 8/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5748 - sparse_categorical_accuracy: 0.7500
Epoch 9/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5743 - sparse_categorical_accuracy: 0.7502
Epoch 10/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5739 - sparse_categorical_accuracy: 0.7506
Epoch 11/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5673 - sparse_categorical_accuracy: 0.7540
Epoch 12/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5649 - sparse_categorical_accuracy: 0.7561
Epoch 13/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 3s 1ms/step - loss: 0.5651 - sparse_categorical_accuracy: 0.7548
Epoch 14/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5618 - sparse_categorical_accuracy: 0.7563
Epoch 15/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5599 - sparse_categorical_accuracy: 0.7571
Epoch 16/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5568 - sparse_categorical_accuracy: 0.7585
Epoch 17/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5556 - sparse_categorical_accuracy: 0.7592
Epoch 18/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5544 - sparse_categorical_accuracy: 0.7595
Epoch 19/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5533 - sparse_categorical_accuracy: 0.7603
Epoch 20/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5532 - sparse_categorical_accuracy: 0.7597
Epoch 21/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5531 - sparse_categorical_accuracy: 0.7602
Epoch 22/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5516 - sparse_categorical_accuracy: 0.7608
Epoch 23/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 3s 1ms/step - loss: 0.5503 - sparse_categorical_accuracy: 0.7611
Epoch 24/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5492 - sparse_categorical_accuracy: 0.7619
Epoch 25/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5482 - sparse_categorical_accuracy: 0.7623
Epoch 26/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5464 - sparse_categorical_accuracy: 0.7635
Epoch 27/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5483 - sparse_categorical_accuracy: 0.7625
Epoch 28/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 3s 1ms/step - loss: 0.5654 - sparse_categorical_accuracy: 0.7555
Epoch 29/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5545 - sparse_categorical_accuracy: 0.7593
Epoch 30/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5512 - sparse_categorical_accuracy: 0.7603
Epoch 31/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5493 - sparse_categorical_accuracy: 0.7616
Epoch 32/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5485 - sparse_categorical_accuracy: 0.7627
Epoch 33/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5593 - sparse_categorical_accuracy: 0.7588
Epoch 34/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5536 - sparse_categorical_accuracy: 0.7608
Epoch 35/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5537 - sparse_categorical_accuracy: 0.7612
Epoch 36/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5518 - sparse_categorical_accuracy: 0.7621
Epoch 37/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5502 - sparse_categorical_accuracy: 0.7618
Epoch 38/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5537 - sparse_categorical_accuracy: 0.7597
Epoch 39/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5526 - sparse_categorical_accuracy: 0.7609
Epoch 40/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5508 - sparse_categorical_accuracy: 0.7608
Epoch 41/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5495 - sparse_categorical_accuracy: 0.7613
Epoch 42/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 3s 1ms/step - loss: 0.5478 - sparse_categorical_accuracy: 0.7625
Epoch 43/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5471 - sparse_categorical_accuracy: 0.7629
Epoch 44/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5462 - sparse_categorical_accuracy: 0.7640
Epoch 45/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5458 - sparse_categorical_accuracy: 0.7633
Epoch 46/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5466 - sparse_categorical_accuracy: 0.7635
Epoch 47/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5492 - sparse_categorical_accuracy: 0.7633
Epoch 48/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5474 - sparse_categorical_accuracy: 0.7639
Epoch 49/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5452 - sparse_categorical_accuracy: 0.7645
Epoch 50/50
1862/1862 ━━━━━━━━━━━━━━━━━━━━ 2s 1ms/step - loss: 0.5446 - sparse_categorical_accuracy: 0.7663
Model training finished
Test accuracy: 77.98%The deep and cross model achieves ~81% test accuracy.
Conclusion
You can use Keras Preprocessing Layers to easily handle categorical features with different encoding mechanisms, including one-hot encoding and feature embedding. In addition, different model architectures — like wide, deep, and cross networks — have different advantages, with respect to different dataset properties. You can explore using them independently or combining them to achieve the best result for your dataset.